重置
序号 ID 年级 类型 来源 摘要 创建时间
20518 5c983a46210b286d125ef639 高中 解答题 高中习题 已知数列 $\{{{a}_{n}}\}$ 是等差数列。证明：
$C_{n}^{0}{{a}_{1}}-C_{n}^{1}{{a}_{2}}+C_{n}^{2}{{a}_{3}}-...+{{(-1)}^{n-1}}C_{n}^{n-1}{{a}_{n}}+{{(-1)}^{n}}C_{n}^{n}{{a}_{n+1}}=0$		 2022-04-17 20:32:00
20517 5c983a80210b286d125ef645 高中 解答题 高中习题 设A是一个有n个元素的集合，A的m个子集 ${{A}_{1}},{{A}_{2}},{{A}_{3}},......,{{A}_{m}}$ 两两互不包含。
求证：（1）$\displaystyle \sum\limits_{i=1}^{m}{\dfrac{1}{C_{n}^{\left| {{A}_{i}} \right|}}}\leqslant 1$（2）$\displaystyle \sum\limits_{i=1}^{m}{C_{n}^{\left| {{A}_{i}} \right|}}\geqslant {{m}^{2}}$		 2022-04-17 20:32:00
20516 5c983a98210b286d074543c1 高中 解答题 高中习题 对任何正整数 $n$，求证：
$\displaystyle \sum\limits_{k=0}^{n}{C_{n}^{k}{{2}^{k}}C_{n-k}^{[\tfrac{n-k}{2}]}}=C_{2n+1}^{n}$
其中 $C_{0}^{0}=1$，$\left[ \dfrac{n-k}{2} \right]$ 表示 $\dfrac{n-k}{2}$ 的整数部分。		 2022-04-17 20:31:00
20515 5c983e82210b286d074543cb 高中 解答题 高中习题 证明：
（1）从前100个正整数中任意取出51个数，都可以找到两个数，它们中的一个是另一个的整数倍；
（2）从前91个正整数中任意取出10个数，则一定有两个数，这两个数中大数不超过小数的1．5倍．		 2022-04-17 20:31:00
20514 5c983e99210b286d074543d1 高中 解答题 高中习题 平面上任作8条直线（互不平行），证明：其中必有两条直线的夹角小于23度．
（2）把1到10这10个正整数摆成一个圆圈，证明：一定存在3个相邻的数之和不小于18．
（3）已给一个由10个互不相等的两位十进制正整数组成的集合．证明：这个集合必有两个无公共元素的非空子集合，这两个子集合中各数之和相等．
（4）100个孩子围成一圈做游戏，其中有41个男孩和59个女孩．证明：一定有两个男孩，他们之间恰好有19个孩子．		 2022-04-17 20:30:00
20513 5c983eb0210b286d125ef64d 高中 解答题 高中习题 已知 ${{a}_{1}},{{a}_{2}},\cdots ,{{a}_{21}}$ 是区间 $\left( 0,400 \right)$ 内的 $21$ 个实数．
证明：总可以找到两个数 ${{a}_{i}},{{a}_{j}}\left( 1\leqslant i<j\leqslant n \right)$，满足 ${{a}_{i}}+{{a}_{j}}<1+2\sqrt{{{a}_{i}}{{a}_{j}}}$．
（2）已知实数 $0<{{a}_{1}}<{{a}_{2}}<\cdots <{{a}_{2011}}$，证明：存在两个数 ${{a}_{i}},{{a}_{j}}\left( 1\leqslant i<j\leqslant 2011 \right)$，满足
${{a}_{j}}-{{a}_{i}}<\dfrac{\left( 1+{{a}_{i}} \right)\left( 1+{{a}_{j}} \right)}{2010}$．		 2022-04-17 20:30:00
20512 5c983ec9210b286d074543d8 高中 解答题 高中习题 从数 $1,2,3,\cdots ,2017$ 中删去一些数，使得剩下的数中任何一个数都不等于其余任意两个不同的数的积，问最少要删去多少个数才能做到这一点？
（2）设 $x,y(x > y)$ 为一组互不相等的正整数 $ a_1,a_2,…,a_n $ 中的任意两个数，满足 $ x – y≥ xy/31$．求此正整数组中数的个数n的最大值．		 2022-04-17 20:29:00
20511 5c983f1b210b286d074543de 高中 解答题 高中习题 任选6人，试证：其中必有3人，他们互相认识或都不认识；
（2）17名科学家中每两名科学家都和其他科学家通信，在他们通信时只讨论三个题目，而且任意两名科学家通信时只讨论一个题目，证明：其中至少有三名科学家，他们相互通信时讨论的是同一个题目．		 2022-04-17 20:29:00
20510 5c983f2e210b286d125ef656 高中 解答题 高中习题 设 $\alpha $ 是正实数，$n$ 为正整数，求证：存在正整数 $p,q$ 使
$\left| \alpha -\dfrac{q}{p} \right|\leqslant \dfrac{1}{np}$ 。		 2022-04-17 20:28:00
20509 5c983f43210b286d125ef65c 高中 解答题 高中习题 若从 $1,2,3,\cdots ,n$ 中任取 $5$ 个两两互素的不同的整数 ${{a}_{1}},{{a}_{2}},{{a}_{3}},{{a}_{4}},{{a}_{5}}$，其中总有一个是素数，求
$n$
的最大值．
（2）设 $S=\left\{ 1,2,\cdots ,2005 \right\}$ $S=\left\{ 1,2,3,\cdots ,2005 \right\}$，若 $S$ 中任意 $n$ 个两两互质的数组成的集合中都至少有一个质数，试求 $n$ n的最小值．		 2022-04-17 20:28:00
20508 5c983f55210b286d125ef662 高中 解答题 高中习题 从4个同心圆的圆心出发的100条射线等分各圆周，分别与4个圆各有100个交点．任意给每个圆上的点染上黑、白两色之一，使每个圆上都恰有50个黑点和50个白点．
证明：可将此4个圆适当旋转，使这100条射线中至少存在13条射线，它们中每一条穿过的4个点颜色都相同．		 2022-04-17 20:28:00
20507 5c998a72210b280b2397e8b2 高中 解答题 高中习题 空间有 $20$ 个点，或是红点，或是蓝点，而且任意四个同色点不共面。证明：四个顶点同色的四面体，这个四面体中有某一侧面不含另一种颜色的点。 2022-04-17 20:27:00
20506 5c998b38210b280b2256bf6f 高中 解答题 高中习题 在 $12\times 12$ 的超级棋盘上，一匹超级马每步从 $3\times 4$ 矩形的一个角跳到不相邻的另一个角．问：能否从任一点出发遍历每一格恰一次，再回到出发点？ 2022-04-17 20:27:00
20505 5c998bfe210b280b2256bf74 高中 解答题 高中习题 把平面上的每个点三染色（红、黄、蓝），证明：存在一条长度为1且端点同色的线段． 2022-04-17 20:26:00
20504 5c998c5d210b280b2397e8bf 高中 解答题 高中习题 在一直线上相邻两点的距离都等于 $1$ 的四个点上各有一只青蛙，允许任意一只青蛙以其余三只青蛙中的某一只为中心跳到其对称点上．
证明：无论跳动多少次后，四只青蛙所在的点中相邻两点之间的距离不能都等于 $2008$．		 2022-04-17 20:26:00
20503 5c998cf7210b280b2397e8c5 高中 解答题 高中习题 一初始时刻黑板上写有两个多项式 ${{x}^{3}}-3{{x}^{2}}+5$ 和 ${{x}^{2}}-4x$．如果黑板上有多项式 $f\left( x \right)$ 和 $g\left( x \right)$，则可以在黑板上写上 $f\left( x \right)\pm g\left( x \right) f\left( x \right)g\left( x \right)$，$f\left( g\left( x \right) \right) cf\left( x \right)$，其中 $c$ 为任意实数．经过有限次操作后，黑板上可否出现多项式 ${{x}^{n}}-1$，其中 $n$ 为某个正整数． 2022-04-17 20:26:00
20502 5c998d4c210b280b2397e8cb 高中 解答题 高中习题 如图，正五边形上的顺次排列 $5$ 个整数 $x_1,x_2,…,x_5$，其和是正的．对其中任意3个连续顶点上的数 $x,y,z$，若中间的 $y < 0$，则作变换 $(x,y,z)→(x + y,– y,y + z)$，只要所得 $5$ 个整数中仍有负的，则继续进行此调整．试证：这种调整只能进行有限次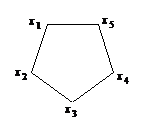． 2022-04-17 20:25:00
20501 5c998e52210b280b2397e8d1 高中 解答题 高中习题 某班有 $47$ 个学生，所用教室有 $6$ 排，每排有 $8$ 个座位，用 $(i,j)$ 表示位于第i排第j列的座位．新学期准备调整座位，设一个学生原来的座位为 $(i,j)$，如果调整后的座位为 $(m,n)$，则称该生作了移动 $[a,b] = [i – m,j – n]$，并称 $a + b$ 为该生的位置数，所有学生的位置数之和记为 $S$．求 $S$ 的最大可能值与最小可能值之差． 2022-04-17 20:24:00
20500 5c998ee6210b280b2256bf7f 高中 解答题 高中习题 （1）在 $2006$ 张纸片的正面各写上整数 $1$ 到 $2006$ 中的一个，然后把纸片反过来弄乱，在纸片的反面同样写上整数1到2006中的一个．问：是否可能这2006张纸片的正反面上数的差（大数减小数）互不相同．
（2）能否把1，1，2，2，3，3，…，1986，1986这些数排成一行，使得两个1之间夹着1个数，两个2之间夹着2个数，两个1986之间夹着1986个数？		 2022-04-17 20:24:00
20499 5c999267210b280b2397e8da 高中 解答题 高中习题 一次考试共有 $m$ 道试题，$n$ 个学生参加，其中 $m,n\geqslant 2$ 为给定的整数。每道题的得分规则是：若改题恰有 $x$ 个学生没有答对，则每个答对改题的学生得 $x$ 分，未答对的学生得零分。每个学生的总分为其 $m$ 道题的得分的总和。将所有学生总分从高到低排列为 ${{p}_{1}}\geqslant {{p}_{2}}\geqslant \cdots \geqslant {{p}_{n}}$，求 ${{p}_{1}}+{{p}_{n}}$ 的最大可能值。 2022-04-17 20:23:00
0.159237s