如图,正五边形上的顺次排列 $5$ 个整数 $x_1,x_2,…,x_5$,其和是正的.对其中任意3个连续顶点上的数 $x,y,z$,若中间的 $y < 0$,则作变换 $(x,y,z)→(x + y,– y,y + z)$,只要所得 $5$ 个整数中仍有负的,则继续进行此调整.试证:这种调整只能进行有限次.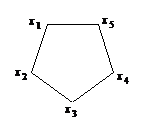
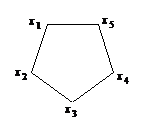
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设五个顶点上的数顺次为 ${{x}_{1}},{{x}_{2}},\cdots ,{{x}_{5}}$ 。构造目标函数
$f({{x}_{1}},{{x}_{2}},\cdots,{{x}_{5}})={{({{x}_{1}}-{{x}_{3}})}^{2}}+{{({{x}_{2}}-{{x}_{4}})}^{2}}+{{({{x}_{3}}-{{x}_{5}})}^{2}}+{{({{x}_{4}}-{{x}_{2}})}^{2}}+{{({{x}_{5}}-{{x}_{2}})}^{2}}$
不妨设 ${{x}_{1}}<0$,则 ${{x}_{1}},{{x}_{2}},\cdots,{{x}_{5}}$ 在操作后,变为 $-{{x}_{1}},{{x}_{1}}+{{x}_{2}},\cdots,{{x}_{5}}+{{x}_{1}}$,这时目标函数的改变量为
$f({{x}_{1}},{{x}_{2}},\cdots,{{x}_{5}})-f(-{{x}_{1}},{{x}_{1}}+{{x}_{2}},\cdots ,{{x}_{5}}+{{x}_{1}})$
$=({{(-{{x}_{1}}-{{x}_{3}})}^{2}}+{{({{x}_{1}}+{{x}_{2}}-{{x}_{4}})}^{2}}+{{({{x}_{3}}-{{x}_{5}}-{{x}_{1}})}^{2}}+{{({{x}_{4}}+{{x}_{1}})}^{2}}+{{({{x}_{5}}-{{x}_{2}})}^{2}})$
$-({{({{x}_{1}}-{{x}_{3}})}^{2}}+{{({{x}_{2}}-{{x}_{4}})}^{2}}+{{({{x}_{3}}-{{x}_{5}})}^{2}}+{{({{x}_{4}}-{{x}_{2}})}^{2}}+{{({{x}_{5}}-{{x}_{2}})}^{2}})$
$=2{{x}_{1}}({{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}})<0$
这表明,没经过一次操作,目标函数 $f$ 的值至少减少2,但因为 $f$ 为整数且 $f\geqslant 0$,故操作只能进行有限次。
$f({{x}_{1}},{{x}_{2}},\cdots,{{x}_{5}})={{({{x}_{1}}-{{x}_{3}})}^{2}}+{{({{x}_{2}}-{{x}_{4}})}^{2}}+{{({{x}_{3}}-{{x}_{5}})}^{2}}+{{({{x}_{4}}-{{x}_{2}})}^{2}}+{{({{x}_{5}}-{{x}_{2}})}^{2}}$
不妨设 ${{x}_{1}}<0$,则 ${{x}_{1}},{{x}_{2}},\cdots,{{x}_{5}}$ 在操作后,变为 $-{{x}_{1}},{{x}_{1}}+{{x}_{2}},\cdots,{{x}_{5}}+{{x}_{1}}$,这时目标函数的改变量为
$f({{x}_{1}},{{x}_{2}},\cdots,{{x}_{5}})-f(-{{x}_{1}},{{x}_{1}}+{{x}_{2}},\cdots ,{{x}_{5}}+{{x}_{1}})$
$=({{(-{{x}_{1}}-{{x}_{3}})}^{2}}+{{({{x}_{1}}+{{x}_{2}}-{{x}_{4}})}^{2}}+{{({{x}_{3}}-{{x}_{5}}-{{x}_{1}})}^{2}}+{{({{x}_{4}}+{{x}_{1}})}^{2}}+{{({{x}_{5}}-{{x}_{2}})}^{2}})$
$-({{({{x}_{1}}-{{x}_{3}})}^{2}}+{{({{x}_{2}}-{{x}_{4}})}^{2}}+{{({{x}_{3}}-{{x}_{5}})}^{2}}+{{({{x}_{4}}-{{x}_{2}})}^{2}}+{{({{x}_{5}}-{{x}_{2}})}^{2}})$
$=2{{x}_{1}}({{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}+{{x}_{5}})<0$
这表明,没经过一次操作,目标函数 $f$ 的值至少减少2,但因为 $f$ 为整数且 $f\geqslant 0$,故操作只能进行有限次。
答案
解析
备注