重置
序号 ID 年级 类型 来源 摘要 创建时间
26878 59128bbee020e7000878f922 高中 解答题 自招竞赛 已知集合 $A = \left\{ \left( {x, y} \right)\left|{{\left( {x - 1} \right)}^2} + {{\left( {y - 2} \right)}^2} \leqslant \dfrac{4}{5} \right.\right\}$，$B = \left\{ {\left( {x, y} \right)\big|\left| {x - 1} \right| + 2\left| {y - 2} \right| \leqslant a} \right\}$，且满足 $A \subseteq B$，求实数 $a$ 的范围． 2022-04-17 20:04:59
26877 59128c04e020e7000a798bbe 高中 解答题 高中习题 已知 $a, b > 0$，求证：$\dfrac{1}{{a + b}} + \dfrac{1}{{a + 2b}} + \cdots + \dfrac{1}{{a + nb}} < \dfrac{n}{{\sqrt {\left( {a + \frac{1}{2}b} \right)\left( {a + \frac{{2n + 1}}{2}b} \right)} }}$． 2022-04-17 20:03:59
26876 59128cc1e020e70007fbedbd 高中 解答题 自招竞赛 已知点 $P\left( {{x_1}, {y_1}} \right)$，将平面坐标系逆时针旋转 $30^\circ $，求新坐标系下点 $P$ 的坐标． 2022-04-17 20:02:59
26875 5912a710e020e7000a798beb 高中 解答题 自招竞赛 设 $OABC$ 是棱长为 $1$ 的正四面体，$OB$ 中点为 $M$，$ON:NC = 1:2$，如图，求过 $A,M,N$ 三点平面与 $O$ 点的距离 $d$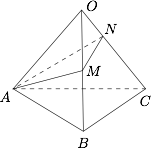． 2022-04-17 20:02:59
26874 5964694ee6a2e7000cc63b80 高中 解答题 自招竞赛 设实数 $\omega>0$，已知函数 $f(x)=\sin^{2}\omega x+\sqrt 3\sin\omega x\cdot \sin\left(\omega x+\dfrac{\pi}{2}\right)$ 的最小正周期是 $\dfrac{\pi}{2}$．求 $f(x)$ 在 $\left[\dfrac{\pi}{8},\dfrac{\pi}{4}\right]$ 上的最大值与最小值． 2022-04-17 20:02:59
26873 59705066dbbeff000706d2c4 高中 解答题 自招竞赛 若实数 $x_{0}$ 满足 $f(x_{0})=x_{0}$，则称 $x=x_{0}$ 为 $f(x)$ 的不动点．已知函数 $f(x)=x^{3}+ax^{2}+bx+3$，其中 $a,b$ 为常数． 2022-04-17 20:01:59
26872 59646eabe6a2e7000bb7ec0c 高中 解答题 自招竞赛 已知 $a$ 为常数，函数 $f(x)=\ln \left(\dfrac {1-x}{1+x}\right)-ax$． 2022-04-17 20:01:59
26871 59646ebbe6a2e7000cc63b92 高中 解答题 自招竞赛 已知不等式 $3\sin ^2x-\cos ^2x+4a\cos x+a^2 \leqslant 31$ 对一切 $x \in \mathbb R$ 恒成立，求实数 $a$ 的取值范围． 2022-04-17 20:00:59
26870 5927cf3b50ce8400087afa41 高中 解答题 高考真题 设集合 $W$ 由满足下列两个条件的数列 $\{a_{n}\}$ 构成：
① $\dfrac{a_{n}+a_{n+2}}{2}<a_{n+1}$；
② 存在实数 $M$，使 $|a_{n}|\leqslant M$．（$n$ 为正整数）		 2022-04-17 20:59:58
26869 59647148e6a2e7000d504815 高中 解答题 自招竞赛 如果双曲线的两个焦点坐标分别为 $F_1(-2,0)$ 和 $F_2(2,0)$，双曲线的一条切线交 $x$ 轴于 $Q\left(\dfrac12,0\right)$，且斜率为 $2$． 2022-04-17 20:59:58
26868 596471d4e6a2e7000d50481a 高中 解答题 自招竞赛 电脑每秒钟以相同的概率输出一个数字 $1$ 或 $2$．将输出的前 $n$ 个数字之和被 $3$ 整除的概率记为 $P_n$．证明： 2022-04-17 20:58:58
26867 597064a1dbbeff0009d29eda 高中 解答题 自招竞赛 电脑每秒钟以相同的概率输出一个数字 $1$ 或 $2$．将输出的前 $n$ 个数字之和被 $3$ 整除的概率记为 $P_n$．证明： 2022-04-17 20:58:58
26866 59647288e6a2e7000a8548d9 高中 解答题 自招竞赛 三次函数 $f(x)=4x^3+ax^2+bx+c$，其中 $a,b,c\in\mathbb R$，满足：当 $-1\leqslant x\leqslant1$ 时，$-1\leqslant f(x)\leqslant 1$，求 $a,b,c$ 的所有可能取值． 2022-04-17 20:58:58
26865 59647bca22a5da00083c22dd 高中 解答题 自招竞赛 如图，$A$ 是两条平行直线 $l_1$，$l_2$ 之间的一个定点，且点 $A$ 到 $l_1$，$l_2$ 的距离分别为 $AM=1$，$AN=\sqrt 3$．设 $\triangle ABC$ 的另两个顶点 $B$，$C$ 分别在 $l_1$，$l_2$ 上运动，且满足 $AB<AC$，$\dfrac {AB}{\cos B}=\dfrac {AC}{\cos C}$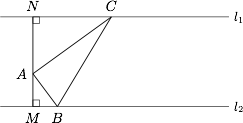． 2022-04-17 20:57:58
26864 59647c0f22a5da000a7a8945 高中 解答题 自招竞赛 如图，已知圆 $O:x^2+y^2=1$ 与 $x$ 轴交于 $A$，$B$ 两点，与 $y$ 轴交于点 $C$，$M$ 是圆 $O$ 上任一点（除去圆 $O$ 与两坐标轴的交点）．直线 $AM$ 与 $BC$ 交于点 $P$，直线 $CM$ 与 $x$ 轴交于点 $N$，设直线 $PM$，$PN$ 的斜率分别为 $m$，$n$，求证：$m-2n$ 为定值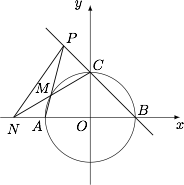． 2022-04-17 20:56:58
26863 59647c3622a5da00083c22e6 高中 解答题 自招竞赛 设 $a_1$，$a_2$，$\cdots$，$a_n$ 均为正实数，$n \in \mathbb N^*$．证明：$$\sum \limits_{k=1}^{n}\dfrac {k^2}{a_1+a_2+\cdots+a_k}<4\sum \limits_{k=1}^{n}\dfrac {k}{a_k}.$$ 2022-04-17 20:55:58
26862 59647cf022a5da00083c22ec 高中 解答题 自招竞赛 已知在 $\triangle ABC$ 中，角 $A,B,C$ 的对边分别为 $a,b,c$，$\triangle ABC$ 的外接圆半径 $R=\sqrt3$，且满足 $\tan B+\tan C=\dfrac{2\sin A}{\cos C}$． 2022-04-17 20:55:58
26861 59647d6322a5da0007aed447 高中 解答题 自招竞赛 如图，在三棱柱 $ABC-A_1B_1C_1$ 中，侧棱 $AA_1\perp\text{平面}ABC$，三角形 $ABC$ 是边长为 $2$ 的等边三角形，$M$ 是 $AA_1$ 上的一点，$AA_1=4$，$A_1M=1$．$P$ 是棱 $BC$ 上一点，且由 $P$ 沿棱柱侧面经过棱 $CC_1$ 到点 $M$ 的最短路线长为 $3\sqrt2$，设这条最短路线与 $CC_1$ 的交点为 $N$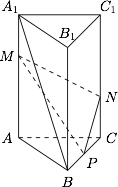． 2022-04-17 20:55:58
26860 59647df822a5da0009864164 高中 解答题 自招竞赛 设数列 $\{a_n\}$ 的前 $n$ 项和为 $S_n$，且满足 $S_2=3$，$2S_n=n+na_n$（$n\in\mathbb N^*$）． 2022-04-17 20:54:58
26859 59647e2b22a5da00083c22f1 高中 解答题 自招竞赛 已知二次函数 $f(x)$ 的二次项系数为 $a$，且不等式 $f(x)>-2x$ 的解集为 $(1,3)$． 2022-04-17 20:54:58
0.178416s