如图,$A$ 是两条平行直线 $l_1$,$l_2$ 之间的一个定点,且点 $A$ 到 $l_1$,$l_2$ 的距离分别为 $AM=1$,$AN=\sqrt 3$.设 $\triangle ABC$ 的另两个顶点 $B$,$C$ 分别在 $l_1$,$l_2$ 上运动,且满足 $AB<AC$,$\dfrac {AB}{\cos B}=\dfrac {AC}{\cos C}$.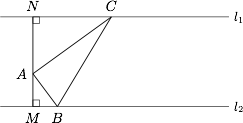

【难度】
【出处】
2014年全国高中数学联赛陕西省预赛(二试)
【标注】
-
试判断 $\triangle ABC$ 的形状,并证明你的结论;标注答案直角三角形解析由 $\dfrac {AB}{\cos B}=\dfrac {AC}{\cos C}$ 及正弦定理,得$$\dfrac {\sin C}{\cos B}=\dfrac {\sin B}{\cos C},$$即$$\sin 2B=\sin 2C.$$因为 $AB<AC$,所以$$\angle C <\angle B, $$故 $2B+2C=\pi$,即$$B+C=\dfrac {\pi}{2},$$因此 $\triangle ABC$ 为直角三角形,且 $\angle A=\dfrac {\pi}{2}$.
-
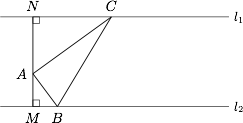
求 $\dfrac {1}{AB}+\dfrac {\sqrt 3}{AC}$ 的最大值.标注答案$\sqrt 2$解析设 $\angle BAM=\theta \left(0<\theta<\dfrac {\pi}{3}\right)$,则$$\angle CAN=\dfrac {\pi}{2}-\theta.$$在 $\mathrm {Rt} \triangle AMB$ 中,$AB=\dfrac {1}{\cos \theta}$;在 $\mathrm {Rt} \triangle ANC$ 中,$AC=\dfrac {\sqrt 3}{\sin \theta}$,所以$$\dfrac {1}{AB}+\dfrac {\sqrt 3}{AC}=\cos\theta+\sin \theta=\sqrt 2\sin \left(\theta+\dfrac {\pi}{4}\right),$$故当 $\theta=\dfrac {\pi}{4}$ 时,$\dfrac {1}{AB}+\dfrac {\sqrt 3}{AC}$ 取得最大值为 $\sqrt 2$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2