设 $OABC$ 是棱长为 $1$ 的正四面体,$OB$ 中点为 $M$,$ON:NC = 1:2$,如图,求过 $A,M,N$ 三点平面与 $O$ 点的距离 $d$.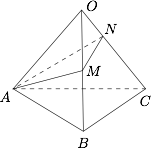

【难度】
【出处】
2006年北京大学自主招生保送生测试
【标注】
【答案】
$\dfrac{{\sqrt {10} }}{10}$
【解析】
用等体积法.因为 $\dfrac{1}{3}{S_{\triangle AMN}} \cdot d = {V_{O - AMN}}$,所以$$d = \frac{{3{V_{O - AMN}}}}{{{S_{\triangle AMN}}}}.$$又$$\frac{{{V_{O - AMN}}}}{{{V_{O - ABC}}}} = \frac{{{V_{A - OMN}}}}{{{V_{A - OBC}}}} = \frac{{{S_{\triangle OMN}}}}{{{S_{\triangle OBC}}}} = \frac{{OM \cdot ON}}{{OB \cdot OC}} = \frac{1}{6},$$所以$${V_{O - AMN}} = \frac{1}{6}{V_{O - ABC}} = \frac{{\sqrt 2 }}{{72}}.$$在 $\triangle AMN$ 中,$AM = \dfrac{{\sqrt 3 }}{2}$,$AN = \sqrt {O{N^2} + O{A^2} - ON \cdot OA} = \dfrac{{\sqrt 7 }}{3}$,$MN = \dfrac{1}{2}AN = \dfrac{{\sqrt 7 }}{6}$.从而有$$\cos \angle ANM = \dfrac{{A{N^2} + M{N^2} - A{M^2}}}{{2 \cdot AN \cdot MN}} = \dfrac{2}{7},$$所以 $\sin \angle ANM = \dfrac{{\sqrt {45} }}{7}$,于是$${S_{\triangle AMN}} = \frac{1}{2}\sin \angle ANM \cdot AN \cdot MN = \frac{1}{2} \cdot \frac{{\sqrt {45} }}{7} \cdot \frac{{\sqrt 7 }}{3} \cdot \frac{{\sqrt 7 }}{6} = \frac{{\sqrt {5} }}{{12}}.$$因此$$d = \frac{{3{V_{O - AMN}}}}{{{S_{\triangle AMN}}}} = \frac{{\sqrt {10} }}{10}.$$
答案
解析
备注