如图，在三棱柱 $ABC-A_1B_1C_1$ 中，侧棱 $AA_1\perp\text{平面}ABC$，三角形 $ABC$ 是边长为 $2$ 的等边三角形，$M$ 是 $AA_1$ 上的一点，$AA_1=4$，$A_1M=1$．$P$ 是棱 $BC$ 上一点，且由 $P$ 沿棱柱侧面经过棱 $CC_1$ 到点 $M$ 的最短路线长为 $3\sqrt2$，设这条最短路线与 $CC_1$ 的交点为 $N$．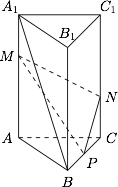
【难度】
【出处】
2012年全国高中数学联赛河北省预赛（高二）
【标注】
-
求证：$A_1B\parallel\text{平面}MNP$；标注答案略解析因为侧棱 $AA_1\perp\text{平面}ABC$，三角形 $ABC$ 是等边三角形，所以侧面均为全等的矩形．
如图，将侧面 $BC_1$ 旋转 $120^\circ$ 使其与侧面 $AC_1$ 在同一平面上，点 $P$ 运动到点 $P_1$ 的位置，连接 $MP_1$，则 $MP_1$ 就是由点 $P$ 沿棱柱侧面经过 $CC_1$ 到点 $M$ 的最短路径．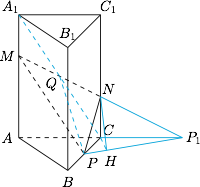
设 $PC=x$，则 $P_1C=x$，在 $\mathrm{Rt}\triangle MAP_1$ 中，$$(2+x)^2+3^2=18,$$所以 $x=1$，故点 $P$ 为 $BC$ 的中点，易知 $NC=1$．
设 $A_1C$ 与 $MN$ 交于点 $Q$，则点 $Q$ 为 $A_1C$ 的中点，所以$$A_1B\parallel PQ,$$故$$A_1B\parallel\text{平面}MNP.$$ -
求平面 $MNP$ 和平面 $ABC$ 所成二面角（锐角）的正切值．标注答案$2$解析连接 $PP_1$，则 $PP_1$ 就是平面 $MNP$ 与平面 $ABC$ 的交线．作 $NH\perp PP_1$ 于 $H$，又$$CC_1\perp\text{平面}CPP_1,$$连接 $CH$，易得$$CH\perp PP_1,$$因此 $\angle NHC$ 就是平面 $NMP$ 与平面 $ABC$ 所成二面角的平面角．
在 $\mathrm{Rt}\triangle PHC$ 中，因为$$\angle PCH=\dfrac12\angle PCP_1=60^\circ,$$所以 $CH=\dfrac12$．
在 $\mathrm{Rt}\triangle NCH$ 中，$$\tan\angle NHC=\dfrac{NC}{CH}=2.$$因此平面 $MNP$ 和平面 $ABC$ 所成二面角（锐角）的正切值为 $2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
