重置
序号 ID 年级 类型 来源 摘要 创建时间
20838 5c74ab75210b28428f14cb28 高中 解答题 自招竞赛 如图21-5所示，在正四面体 $ABCD$ 中，点 $O$，$P Q R$ 分别是四个面的中心，连接 $OPQR$ 跟构成另一个正四面体．两个正四面体 $OPQR$ 与 $ABCD$ 的体积比是 $m \mathsf{:} n$，其中 $m n$ 为互素的正整数，求 $m+n$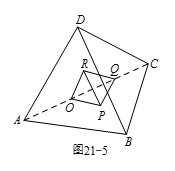． 2022-04-17 20:28:03
20837 5c74ab7e210b284290fc22a7 高中 解答题 自招竞赛 用一块直径是12英寸的圆柱形元木做一个楔子，从同一点开始截，需要截两次．第一个截面垂直于圆木的轴，第二个截面与第一个截面成 $45{}^\circ $ 角，这个楔子的体积可以表示为 $n\text{ }\!\!\pi\!\!\text{}$ 的形式，其中 $n$ 是一个正整数．求 $n$． 2022-04-17 20:28:03
20836 5c74ab91210b28428f14cb2e 高中 解答题 自招竞赛 已知在菱形 $ABCD$ 中，$\vartriangle ABD$ 与 $\vartriangle ACD$ 的外接圆半径分别为 $12.5$ 与25．求菱形 $ABCD$ 的面积． 2022-04-17 20:27:03
20835 5c74ab9a210b284290fc22b4 高中 解答题 自招竞赛 数列 $1440 ,1916, 1848 ,\cdots $ 是由两个等差数列将对应项相乘而得，求此数列的第8项． 2022-04-17 20:27:03
20834 5c74abaa210b284290fc22ba 高中 解答题 自招竞赛 设 $a b c$ 是三个正整数，满足 $a=b+60$，$\sqrt{a}+\sqrt{b}=\sqrt{c}$，且 $\sqrt{c}$ 不是整数（即 $c$ 不是一个完全平方数）．令 $s=a+b$，求 $s$ 的最大可能值． 2022-04-17 20:27:03
20833 5c74abb1210b284290fc22c0 高中 解答题 自招竞赛 如图21-6所示，在 $\operatorname{Rt}\vartriangle ABC$ 中，$\angle C$ 是直角，$AC=7$，$BC=24$．点 $M$ 是边 $AB$ 的中点．平面上一点 $D$ 满足 $AD=BD=15$．设 $\vartriangle CDM$ 的面积可以表示为 $\frac{m\sqrt{n}}{p}$ 的形式，其中 $m n p$ 都是正整数，$m p$ 互素，且 $n$ 不能被任何素数的平方整除．求 $m+n+p$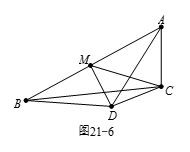． 2022-04-17 20:27:03
20832 5c74abba210b28428f14cb3a 高中 解答题 自招竞赛 一个学校社团投票选举社长，有27个候选人，每个成员（包括候选人）只能投一票，支持其中的一位．对于每个候选人，他的得票率的100倍至少比他的票数少1．这个社团至少有多少人？ 2022-04-17 20:26:03
20831 5c74abc2210b284290fc22c6 高中 解答题 自招竞赛 已知虫子从一个等边三角形的一个顶点出发，每次虫子随机等可能地爬向除自己所在定点另外两个顶点中的一个．假设虫子爬行10次后恰回到出发点的概率为 $\frac{m}{n}$，其中 $m n$ 为互素的正整数，求 $m+n$． 2022-04-17 20:26:03
20830 5c74abcb210b284290fc22cb 高中 解答题 自招竞赛 设 $A\left( 0 ,0 \right) B\left( b ,2 \right)$ 为坐标平面上的点，凸六边形 $ABCDEF$ 的各边长度相等，$AB\parallel DE BC\parallel EF CD\parallel FA$，$\angle FAB=120{}^\circ $，六个顶点的纵坐标分别为 $0,2 ,4 ,6 ,8, 10$（不一定按照顺序）．这个六边形的面积可以表示为 $m\sqrt{n}$，其中 $m n$ 为正整数，$n$ 不能被任何素数的平方整除，求 $m+n$． 2022-04-17 20:25:03
20829 5c74b7ef210b284290fc230d 高中 解答题 自招竞赛 十进制下的四位正整数 $n$ 是由四个连续的整数按从左到右递减顺序排列而成，求 $n$ 被 $37$ 除时所有可能的余数之和。 2022-04-17 20:25:03
20828 5c74b7f9210b28428f14cb7a 高中 解答题 自招竞赛 凸多面体 $P$ 有 $26$ 个顶点、$60$ 条边、$36$ 个面，其中 $24$ 个面是三角形，$12$ 个面是四边形。空间对角线是指连接不在同一平面上互不相邻的两个顶点之间的线段，问 $p$ 有多少条这样的空间对角线。 2022-04-17 20:25:03
20827 5c74b7fe210b284290fc2318 高中 解答题 自招竞赛 正方形 $ABCD$ 的边长为 $2$ 。 $S$ 是所有长度为 $2$，且两个端点在正方形相邻两边上的线段组成的集合。 $S$ 中每条线段的中点围成了一个图形，设这个图形的面积（精确到百分位））为 $k$，求 $100k$ 。 2022-04-17 20:24:03
20826 5c74b805210b284290fc231e 高中 解答题 自招竞赛 $\text{Alpha}$ 和 $\text{Beta}$ 两个人参加了为期两天的问题求解竞赛，每个人在两天中要解答的问题满分共为 $500$ 分。 $\text{Alpha}$ 在第一天满分 $300$ 分的问题解答中获得 $160$ 分，在第二天满分为 $200$ 分的问题解答中获得 $140$ 分。 $\text{Beta}$ 第一天要解答的问题满分不是 $300$ 分，但两天中的每一天他都获得了一个正整数分数，另外，$\text{Beta}$ 每一天的正确率都低于 $\text{Alpha}$ 。 $\text{Alpha}$ 两天的平均正确率是 $\frac{300}{500}=\frac{3}{5}$ 。设 $\text{Beta}$ 两天平均正确率的最大可能值是 $\frac{m}{n}$，其中 $m$，$n$ 是互素的正整数，求 $m+n$ 。 2022-04-17 20:24:03
20825 5c74b818210b284290fc232a 高中 解答题 自招竞赛 $n$ 条线段 ${{P}_{1}}{{P}_{2}}$，${{P}_{2}}{{P}_{3}}$，…，${{P}_{n}}{{P}_{1}}$ 相交成一个正 $n$ 角星，当且仅当它们满足下列条件：
（1）点 ${{P}_{1}}$，${{P}_{2}}$，…，${{P}_{n}}$ 在同一平面上，且任三点不共线；
（2）这 $n$ 条线段中的任一条至少与其他线段中的某一条有一个公共内点；
（3）点 ${{P}_{1}}$，${{P}_{2}}$，…，${{P}_{n}}$ 处的角相等；
（4）线段 ${{P}_{1}}{{P}_{2}}$，${{P}_{2}}{{P}_{3}}$，…，${{P}_{n}}{{P}_{1}}$ 长度相等；
（5）在每个顶点处，${{P}_{1}}{{P}_{2}}$，${{P}_{2}}{{P}_{3}}$，…，${{P}_{n}}{{P}_{1}}$ 的轨迹以小于180度的角沿逆时针方向运行。
没有正三角星、正四角星、正六角星，所有的正五角星彼此相似，但有两个互不相似的正七角星。求有多少个毫不相似的正 $1000$ 角星。		 2022-04-17 20:23:03
20824 5c74b821210b284290fc2330 高中 解答题 自招竞赛 $\vartriangle ABC$ 的三边长分别是 $3$，$4$，$5$，矩形 $DEFG$ 的长为 $7$，宽为 $6$ 。线段 ${{s}_{1}}$ 把 $\vartriangle ABC$ 分割成三角形 ${{U}_{1}}$ 和梯形 ${{V}_{1}}$；线段 ${{s}_{2}}$ 把矩形 $DEFG$ 分为三角形 ${{U}_{2}}$ 和梯形 ${{V}_{2}}$，且 ${{U}_{1}}\sim {{U}_{2}}$，${{V}_{1}}\sim {{V}_{2}}$ 。若三角形 ${{U}_{1}}$ 面积的最小值为 $\frac{m}{n}$，其中 $m$，$n$ 是互素的正整数，求 $m+n$ 。 2022-04-17 20:23:03
20823 5c74b826210b284290fc2336 高中 解答题 自招竞赛 矩形 $ABCD$ 的长为 $36$，宽为 $15$ 。现把一个半径为 $1$ 的圆完全随机地放在矩形内，假设该圆与对角线 $AC$ 不相交的概率为 $\frac{m}{n}$，其中 $m$，$n$ 是互素的正整数，求 $m+n$ 。 2022-04-17 20:22:03
20822 5c74b82b210b28428f14cb87 高中 解答题 自招竞赛 一个圆锥高为 $4$，底面半径为 $3$，它的表面被涂上了油漆。有一平行于底面的平面把该圆锥截为一个略小的圆锥 $C$ 和个圆台 $F$，截得的圆锥 $C$ 涂油漆的面积与圆台 $F$ 涂油漆的面积之比为 $k$，圆锥 $C$ 与圆台 $F$ 的体积之比也是 $k$ 。假设 $k=\frac{m}{n}$，其中 $m$，$n$ 是互素的正整数，求 $m+n$ 。 2022-04-17 20:21:03
20821 5c74b831210b28428f14cb8c 高中 解答题 自招竞赛 令 $S$ 是满足 $0\leqslant x\leqslant 1$，$0\leqslant y\leqslant 1$，且 $\left[ {{\log }_{2}}\left( \frac{1}{x} \right) \right]$ 与 $\left[ {{\log }_{5}}\left( \frac{1}{y} \right) \right]$ 均为偶数的坐标 $\left( x, y \right)$ 组成的集合。
假设集合 $S$ 表示的图形面积为 $\frac{m}{n}$，其中 $m$，$n$ 是互素的正整数，求 $m+n$ 。 $\left[ z \right]$ 表示小于或等于实数 $z$ 的最大整数。		 2022-04-17 20:21:03
20820 5c74b83f210b284290fc2343 高中 解答题 自招竞赛 用一条 $20$ 英尺的长绳将一只麒麟从圆柱形实心魔塔底部吊起，魔塔半径为 $8$ 英尺。该绳一端拴在塔的底面圆周上，另一端拴着距离地面 $4$ 英尺高的麒麟，绳子绷得很紧，绳的末端（拴着麒麟的一端）距离绳接触塔的最近点为 $4$ 英尺。设接触塔的绳长 $\frac{a-\sqrt{b}}{c}$ 英尺，其中 $a$，$b$，$c$ 是正整数，且 $c$ 是素数。求 $a+b+c$ 。 2022-04-17 20:20:03
20819 5c74b845210b28428f14cb92 高中 解答题 自招竞赛 定义在正整数集上的函数 $f\left( x \right)=\left\{ \begin{align}
& 1,x=1 \\
& x/10,x被10整除 \\
& x+1,其他 \\
\end{align} \right.$ 对于任意正整数 $x$，我们定义数列 $\left\{ {{x}_{n}} \right\}$
如下：${{x}_{1}}=x,{{x}_{n+1}}=f\left( {{x}_{n}} \right),n\in {{N}^{+}}$ 。定义 $d\left( x \right)$ 为满足 ${{x}_{n}}=1$ 的最小的 $n$ 。例如，$d\left( 100 \right)=3 d\left( 87 \right)=7$ 。设 $m$ 是满足 $d\left( x \right)=20$ 的正整数 $x$ 的个数，求 $m$ 的所有不同素因数之和。		 2022-04-17 20:20:03
0.179243s