已知在菱形 $ABCD$ 中,$\vartriangle ABD$ 与 $\vartriangle ACD$ 的外接圆半径分别为 $12.5$ 与25.求菱形 $ABCD$ 的面积.
【难度】
【出处】
2003年第21届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
400
【解析】
如图21-10所示,设 $O$ 为线段 $AC BD$ 的交点,$E$ 为 $\vartriangle ABD$ 的外接圆与直线 $AC$ 的交点,延长 $DB$ 交 $\vartriangle ACD$ 的外接圆于 $F$,则由圆幂定理得 $AO\cdot OE=BO\cdot OD$,$DO\cdot OF=AO\cdot OC$.
设 $AC=2m$,$BD=2n$,由于 $AE$ 是 $\vartriangle ABD$ 外接圆的直径,$DF$ 是 $\vartriangle ACD$ 外接圆的直径,所以上面两个等式可以化为
$m\left(25-m \right)={{n}^{2}}\Rightarrow 25m={{m}^{2}}+{{n}^{2}}$,
$n\left(50-n \right)={{m}^{2}}\Rightarrow 50n={{m}^{2}}+{{n}^{2}}$.
因此 $m=2n$,并可推得 $m=20$,$n=10$.故 ${{S}_{ABCD}}\text{=}\frac{1}{2}\cdot AC\cdot BD=2mn=400$.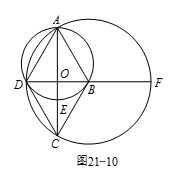
设 $AC=2m$,$BD=2n$,由于 $AE$ 是 $\vartriangle ABD$ 外接圆的直径,$DF$ 是 $\vartriangle ACD$ 外接圆的直径,所以上面两个等式可以化为
$m\left(25-m \right)={{n}^{2}}\Rightarrow 25m={{m}^{2}}+{{n}^{2}}$,
$n\left(50-n \right)={{m}^{2}}\Rightarrow 50n={{m}^{2}}+{{n}^{2}}$.
因此 $m=2n$,并可推得 $m=20$,$n=10$.故 ${{S}_{ABCD}}\text{=}\frac{1}{2}\cdot AC\cdot BD=2mn=400$.

答案
解析
备注