查看数据源：5c74ab7e210b284290fc22a7
用一块直径是12英寸的圆柱形元木做一个楔子，从同一点开始截，需要截两次．第一个截面垂直于圆木的轴，第二个截面与第一个截面成 $45{}^\circ $ 角，这个楔子的体积可以表示为 $n\text{ }\!\!\pi\!\!\text{}$ 的形式，其中 $n$ 是一个正整数．求 $n$．
【难度】
【出处】
2003年第21届美国数学邀请赛Ⅱ（AIMEⅡ）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的截面
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的体积
【答案】
216
【解析】
如图21-8所示，设 $AB$ 为第一个截面的直径，$AC$ 为第二个截面最长的弦．$\vartriangle ABC$ 为一个等腰直角三角形，$AB=BC=12$ 英寸．如果过 $C$ 点垂直于圆木的轴再作一个截面，就又得到一个楔子，这两个楔子拼合起来恰好是一个底面直径为12英寸，高为12英寸的圆柱体，所以楔子的体积为 $V=\frac{1}{2}\left( \text{}\!\!\pi\!\!\text{ }{{\left( \frac{12}{2} \right)}^{2}}\cdot 12 \right)=216\text{}\!\!\pi\!\!\text{ }$，
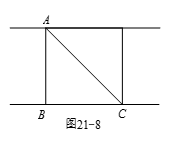
所以 $n=216$．
答案 解析 备注
0.113871s