如图21-5所示,在正四面体 $ABCD$ 中,点 $O$,$P Q R$ 分别是四个面的中心,连接 $OPQR$ 跟构成另一个正四面体.两个正四面体 $OPQR$ 与 $ABCD$ 的体积比是 $m \mathsf{:} n$,其中 $m n$ 为互素的正整数,求 $m+n$.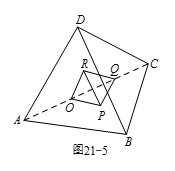

【难度】
【出处】
2003年第21届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
28
【解析】
由图21-7可知,点 $O P$ 分别为 $\vartriangle DAB$ 与 $\vartriangle ABC$ 的中心,连接 $DO$ 并延长,交线段 $AB$ 与 $M$.因为 $ABCD$ 为正四面体,所以 $M$ 是 $AB$ 的中点,可知 $DO$ 垂直 $AB$ 于 $M$,$CP$ 垂直 $AB$ 于 $M$.由于 $\frac{MO}{MD}=\frac{MP}{MC}=\frac{1}{3}$,故 $\Delta MOP\sim\Delta MDC$,且相似比为 $1 \mathsf{:} 3$.因此两个正四面体的相似比也为 $1 \mathsf{:} 3$,故 $\frac{m}{n}={{\left(\frac{1}{3} \right)}^{3}}=\frac{1}{27}$,即 $m+n=28$.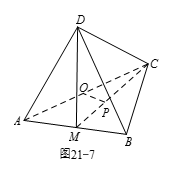

答案
解析
备注