用一条 $20$ 英尺的长绳将一只麒麟从圆柱形实心魔塔底部吊起，魔塔半径为 $8$ 英尺。该绳一端拴在塔的底面圆周上，另一端拴着距离地面 $4$ 英尺高的麒麟，绳子绷得很紧，绳的末端（拴着麒麟的一端）距离绳接触塔的最近点为 $4$ 英尺。设接触塔的绳长 $\frac{a-\sqrt{b}}{c}$ 英尺，其中 $a$，$b$，$c$ 是正整数，且 $c$ 是素数。求 $a+b+c$ 。
【难度】
【出处】
2004年第22届美国数学邀请赛Ⅰ（AIMEⅠ）
【标注】
【答案】
813
【解析】
如图22-3所示，假定绳子挂住的魔塔底端一点为 $A$ 点，接触塔最后的点为 $P$ 点，把麒麟吊在 $Q$ 点、点 $S$，$T$ 分别是点 $P$，$Q$ 在地面的投影，$O$ 点在塔的中轴上，$R$ 是 $Q$ 垂直下方一点，使得 $\vartriangle OPR$ 所在的平面与地面平行。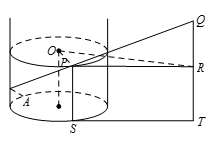
由于 $OP$ 是塔的半径，故 $OP=8$ 。
因为 $Q$ 到塔的距离为 $4$ 英尺，故 $OR=12$，又由于 $\angle OPR$ 是直角，因此 $PR=4\sqrt{5}$ 。
如果塔壁伸展平与 $P Q S T$ 共面，则 $\text{Rt}\vartriangle PQR\sim \text{Rt}\vartriangle AQT$
因此我们有
$\frac{PQ}{PR}=\frac{AQ}{AT}=\frac{20}{\sqrt{{{20}^{2}}-{{4}^{2}}}}=\frac{5}{\sqrt{{{5}^{2}}-{{1}^{2}}}}=\frac{5}{2\sqrt{6}}$ 。
其中 $AQ$ 是点 $A$ 与点 $Q$ 之间的绳长，$AT$ 是 $AQ$ 绳长在地面的射影。
因此 $PQ=\frac{5}{2\sqrt{6}}\cdot4\sqrt{5}=\frac{5\sqrt{30}}{3}$，故与塔壁接触的绳长为 $20-\frac{5\sqrt{30}}{3}=\frac{60-\sqrt{750}}{3}$，故 $a+b+c=60+750+3=813$ 。
由于 $OP$ 是塔的半径，故 $OP=8$ 。因为 $Q$ 到塔的距离为 $4$ 英尺，故 $OR=12$，又由于 $\angle OPR$ 是直角，因此 $PR=4\sqrt{5}$ 。
如果塔壁伸展平与 $P Q S T$ 共面，则 $\text{Rt}\vartriangle PQR\sim \text{Rt}\vartriangle AQT$
因此我们有
$\frac{PQ}{PR}=\frac{AQ}{AT}=\frac{20}{\sqrt{{{20}^{2}}-{{4}^{2}}}}=\frac{5}{\sqrt{{{5}^{2}}-{{1}^{2}}}}=\frac{5}{2\sqrt{6}}$ 。
其中 $AQ$ 是点 $A$ 与点 $Q$ 之间的绳长，$AT$ 是 $AQ$ 绳长在地面的射影。
因此 $PQ=\frac{5}{2\sqrt{6}}\cdot4\sqrt{5}=\frac{5\sqrt{30}}{3}$，故与塔壁接触的绳长为 $20-\frac{5\sqrt{30}}{3}=\frac{60-\sqrt{750}}{3}$，故 $a+b+c=60+750+3=813$ 。
答案
解析
备注
