重置
序号 ID 年级 类型 来源 摘要 创建时间
21038 5c6bd2ef210b281db9f4c8ff 高中 解答题 自招竞赛 在梯形 $ABCD$ 中，$AB=92$，$BC=50$，$CD=19$，$AD=70$，$AB$ 平行于 $CD$，以 $AB$ 上的点 $P$ 为圆心的圆与 $BC$ 和 $AD$ 相切．已知 $AP=\frac{m}{n}$，其中 $m$ 和 $n$ 是互素的正整数，求 $m+n$． 2022-04-17 20:18:05
21037 5c6bd2f7210b281db9f4c905 高中 解答题 自招竞赛 考虑复平面中使得 $\frac{z}{40}$ 和 $\frac{40}{\overline{z}}$ 的实部和虚部都在0和1之间（包括0和1）的所有 $z$ 组成的区域 $A$．最接近区域 $A$ 的面积的整数是多少？（如果 $z=x+\text{i}y$，其中 $x$ 和 $y$ 是实数，则 $\overline{z}=x-\text{i}y$ 是 $z$ 的共轭） 2022-04-17 20:18:05
21036 5c6bd2fc210b281dbaa934dc 高中 解答题 自招竞赛 直线 ${{l}_{1}}$ 和 ${{l}_{2}}$ 均通过原点，与 $x$ 轴的正半轴在第一象限中分别形成 $\frac{\text{ }\!\!\pi\!\!\text{ }}{70}$ 和 $\frac{\text{ }\!\!\pi\!\!\text{ }}{54}$ 的夹角．对于任意一条直线 $l$ 进行变换，记该变换为 $R$，得到另一条直线 $R\left( l \right)$，变换 $R$ 为：$l$ 先经 ${{l}_{1}}$ 反射，所得直线（即以 ${{l}_{1}}$ 为对称轴，$l$ 的轴对称图形）再经 ${{l}_{2}}$ 反射，得到 $R\left( l \right)$．令 ${{R}^{(1)}}\left( l \right)=R\left( l \right)$；对于 $n\geqslant 2$，定义 ${{R}^{\left( n \right)}}\left( l \right)=R\left( {{R}^{\left( n-1 \right)}}\left( l \right) \right)$．已知直线 $l$ 为 $y$，$y=\frac{19}{92}x$，求使得 ${{R}^{\left( m \right)}}\left( l \right)=l$ 的最小正整数 $m$． 2022-04-17 20:17:05
21035 5c6bd302210b281db9f4c90a 高中 解答题 自招竞赛 在Chomp游戏中，两人轮流从 $5\times 7$ 个方格拼成的矩形板上拿取方格，每次从剩余的方格中选择一个方格，且“吃掉”（拿掉）它，同时由这个方格的左边（向上方的延长线）和下边（向右边的延长线）限定的范围内的所有方格也将一起被“吃掉”．例如，当拿掉图中阴影方格时，四个带有“$\times $”的方格也将拿掉（那些由两条或两条以上虚线所确定的方格在这之前已被拿掉了）．游戏的目标是迫使对方去“吃掉”最后一个方格．以方格为元素组成一个 $5\times 7$ 的方格集合，游戏进行中的每一步所剩下的方格是这个集合的一个子集，图中所示的方格集（除去有虚线为边的方格）便是游戏过程中众多子集中的一个．那么这样的子集共有多少个，包括整个矩形（$5\times 7$ 个方格全体）和空板（空集）在内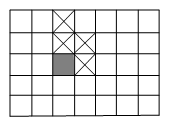？ 2022-04-17 20:17:05
21034 5c6bd30d210b281db9f4c90f 高中 解答题 自招竞赛 在三角形 $ABC$ 中，$AB=9$，$BC:CA=40:41$．这个三角形面积的最大值是多少？ 2022-04-17 20:16:05
21033 5c6bd313210b281db9f4c915 高中 解答题 自招竞赛 在三角形 $ABC$ 中，${A}'$，${B}'$ 和 ${C}'$ 分别在 $BC$，$AC$ 和 $AB$ 上，$A{A}'$，$B{B}'$ 和 $C{C}'$ 相交于一点 $O$，并且 $\frac{AO}{O{A}'}+\frac{BO}{O{B}'}+\frac{CO}{O{C}'}=92$，求 $\frac{AO}{O{A}'}\cdot \frac{BO}{O{B}'}\cdot \frac{CO}{O{C}'}$ 的值． 2022-04-17 20:15:05
21032 5c6bd319210b281db9f4c91b 高中 解答题 自招竞赛 对于正整数 $n$，如果存在某个正整数 $m$，使得 $m!$ 的十进制表示中的末尾恰好有 $n$ 个零，那么就称 $n$ 是“阶乘尾零数”．在小于1992的正整数中有多少个不是“阶乘尾零数”？ 2022-04-17 20:15:05
21031 5c6cbdb7210b281db9f4c930 高中 解答题 自招竞赛 在4000和7000之间4个数位的数字各不相同的偶数有多少？ 2022-04-17 20:14:05
21030 5c6cbdbc210b281db9f4c936 高中 解答题 自招竞赛 一次竞选中，某候选人在国内安排了竞选旅行，我们不妨设他乘飞机．第一天他到正东方某地，第二天接着向正北方向飞到某地，第三天接着向正西方飞到某地，第四天接着向正南方飞到某地，第五天他接着又向正东方飞到某地……如果第 $n$ 天他飞行程为 $\frac{{{n}^{2}}}{2}$ 英里，问从他的出发点到第40天旅行的终点共有多少英里？ 2022-04-17 20:13:05
21029 5c6cbdc3210b281db9f4c93c 高中 解答题 自招竞赛 如表显示了某次钓鱼比赛的结果，上行的值表示钓到的鱼数，下行的值表示钓到 $n$ 条鱼的参赛人数．\[\begin{matrix}\hline
n& 0 & 1 & 2 & 3 & \cdots & 13 & 14 & 15 \\\hline
n& 9 & 5 & 7 & 23 & \cdots & 5 & 2 & 1 \\\hline
\end{matrix}\]当天的报纸对这次比赛作了如下报道：
（1）获胜者钓到15条鱼；
（2）对钓到3条或3条以上的鱼的所有参赛者来说，每人平均钓到6条鱼；
（3）对钓到12条或12条以下的鱼的所有参赛者来说，每人平均钓到5条鱼．
问本次比赛钓到的鱼的总数是多少？		 2022-04-17 20:13:05
21028 5c6cbdcb210b281db9f4c942 高中 解答题 自招竞赛 如果 $0<a<b<c<d<500$，并且 $a+d=b+c$，$bc-ad=93$，那么满足以上条件的有序四元整数组 $\left( a, b, c ,d \right)$ 有多少？ 2022-04-17 20:12:05
21027 5c6cbdde210b281dbaa934f6 高中 解答题 自招竞赛 求满足下列条件的最小正整数：它既可以表示为9个连续正整数之和，又可以表示为10个连续正整数之和，还可以表示为11个连续正整数之和． 2022-04-17 20:12:05
21026 5c6cbde4210b281dbaa934fb 高中 解答题 自招竞赛 从 $\left\{ 1 ,2 ,3, \cdots ,1000 \right\}$ 中随机地取出3个数 ${{a}_{1}}$，${{a}_{2}}$，${{a}_{3}}$，然后再从余下的97个数中随机地取出3个数 ${{b}_{1}}$，${{b}_{2}}$，${{b}_{3}}$，得到一个以 ${{a}_{1}}$，${{a}_{2}}$，${{a}_{3}}$ 为长、宽、高的长方体砖，得到一个以 ${{b}_{1}}$，${{b}_{2}}$，${{b}_{3}}$ 为长、宽、高的长方体盒子，设 $p$ 是可以将砖完全放在盒子中且砖的各面分别与盒子的某些面平行的概率．若 $p$ 是一个最简分数，其分子与分母的和是多少？ 2022-04-17 20:11:05
21025 5c6cbdea210b281db9f4c94e 高中 解答题 自招竞赛 设 $S$ 是一个含有6个元素的集合，共有多少种方法可以得到 $S$ 中的两个子集（这两个子集可能是相同的）使其并为 $S$？这里不考虑两个子集的顺序，即，例如子集对 $\left\{ a ,c \right\}$，$\left\{ b ,c ,d ,e, f \right\}$ 与子集对 $\left\{ b ,c ,d ,e ,f \right\}$，$\left\{ a ,c \right\}$ 被看成是相同的． 2022-04-17 20:11:05
21024 5c6cbdf6210b281dbaa93501 高中 解答题 自招竞赛 在给定圆的圆周上有2000个点，任取一点标上数1，按顺时针方向在标有1的点后数两个点，在第二个点上标上数2，从标有2的点后数3个点，在第三个点上标上数3（如图）．继续这个过程，分别标出1，2，…，1993，在圆周上的这些点中，有些点可能被标上多个数，有些点可能没有被标数，问标有数1993的那个点上被标出的最小数是多少？ 2022-04-17 20:10:05
21023 5c6cbe08210b281dbaa9350c 高中 解答题 自招竞赛 Alfred和Bonnie一起玩一种轮流投掷硬币的游戏，每一盘游戏的胜者是第一个投出人头像的人（硬币一面是人头像图案，另一面是景物图案），他们约定：这一盘的胜者在下盘中第二个投掷．设Alfred在第一盘游戏中先投，设他赢得第六盘游戏的概率是 $\frac{m}{n}$，若 $\frac{m}{n}$ 表示为最简分数，求 $m+n$ 的最后的三位数．（例如1842的最后三位数是842，8032的最后三位数是032）． 2022-04-17 20:09:05
21022 5c6cbe14210b281db9f4c955 高中 解答题 自招竞赛 $\vartriangle ABC$ 的顶点为 $A\left( 0 ,0 \right)$，$B\left( 0 ,420 \right)$ 和 $C\left( 560 ,0 \right)$，一个骰子的六个面中，有两个面刻有 $A$ 字，两个面刻有 $B$ 字，两个面刻有 $C$ 字，点 ${{P}_{1}}\left( k, m \right)$ 位于 $\vartriangle ABC$ 的内部，其他点 ${{P}_{2}}$，${{P}_{3}}$，${{P}_{4}}$，…是按下面的规定通过反复投掷骰子产生的．在 ${{P}_{n}}$ 确定之后如果投出的骰子显示字 $L\left( L\in \left\{ A ,B, C \right\} \right)$，那么 ${{P}_{n+1}}$ 为线段 ${{P}_{n}}L$ 的中点，设 ${{P}_{7}}\left( 14 ,92 \right)$，求 $k+m$． 2022-04-17 20:09:05
21021 5c6cbe1e210b281dbaa93512 高中 解答题 自招竞赛 Jenny和Kenny正沿着相同的方向在两条相距为200英尺的平行的街道上行走，Kenny每秒钟走3英尺，Jenny每秒钟走1英尺，两条街道之间有一个圆柱形的建筑物，直径为100英尺，而圆心到两条街道的距离相等．当建筑物开始遮住Jenny和Kenny的彼此视线的时候，他们相距200英尺，经 $t$ 时间（单位是秒）他们又可以相互看到了，若 $t$ 被写成最简分数，求分子与分母的和． 2022-04-17 20:09:05
21020 5c6cbe24210b281db9f4c95b 高中 解答题 自招竞赛 如果一个矩形的四个顶点分别位于另一个大矩形的四条边上，则称其为大矩形的内接矩形，如果给定大矩形的内接矩形可以绕其中心在大矩形内旋转，则称之为可脱离的内接矩形．给定一个边长分别为6和8的矩形，在其所有可脱离的内接矩形的周长中，最小周长有 $\sqrt{N}$ 的形式，其中 $N$ 是正整数，求 $N$． 2022-04-17 20:08:05
21019 5c6cbe2b210b281db9f4c960 高中 解答题 自招竞赛 设 $GH$ 是 $\vartriangle ABC$ 的一条高线，$R$ 和 $S$ 分别为 $\vartriangle AHC$ 和 $\vartriangle BHC$ 的内切圆与 $CH$ 的切点．若 $AB=1995$，$AC=1994$，$BC=1993$，则 $RS$ 可以被表示为一个最简分数 $\frac{m}{n}$，求 $m+n$ 的值． 2022-04-17 20:07:05
0.157440s