考虑复平面中使得 $\frac{z}{40}$ 和 $\frac{40}{\overline{z}}$ 的实部和虚部都在0和1之间（包括0和1）的所有 $z$ 组成的区域 $A$．最接近区域 $A$ 的面积的整数是多少？（如果 $z=x+\text{i}y$，其中 $x$ 和 $y$ 是实数，则 $\overline{z}=x-\text{i}y$ 是 $z$ 的共轭）
【难度】
【出处】
1992年第10届美国数学邀请赛（AIME）
【标注】
【答案】
572
【解析】
设 $z=x+\text{i}y$．当 $z$ 在试题所述的区域中变化时，有 $0\leqslant x\leqslant 40$，$0\leqslant y\leqslant 40$．如图所示，因 $z$ 的区域包含在以 $\left( 0 ,0 \right)$，$\left( 40 ,0\right)$，$\left( 40 ,40 \right)$，$\left( 0 ,40\right)$ 为顶点的正方形内，同时注意到 $\frac{40}{\overline{z}}=\frac{40}{x-\text{i}y}=\frac{40x}{{{x}^{2}}+{{y}^{2}}}+\text{i}\frac{40y}{{{x}^{2}}+{{y}^{2}}}$，可知对 $\frac{40}{\overline{z}}$ 实部和虚部的限制分别为 $0\leqslant\frac{40x}{{{x}^{2}}+{{y}^{2}}}\leqslant 1$，$0\leqslant\frac{40y}{{{x}^{2}}+{{y}^{2}}}\leqslant 1$．由此知 ${{\left( x-20\right)}^{2}}+{{y}^{2}}\geqslant {{20}^{2}}$，${{x}^{2}}+{{\left(y-20 \right)}^{2}}\geqslant {{20}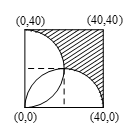^{2}}$．
也就是说试题中所述的区域应在以 $\left(20, 0 \right)$ 为圆心，以20为半径的圆的外部，同时也在以 $\left( 0, 20 \right)$ 为圆心以20为半径的圆的外部；即在图中阴影标出的部分．按图中所示，$A$ 的面积为总面积的 $\frac{3}{4}$（总面积减去图中虚线所示的小正方形的面积）减去两个 $\frac{1}{4}$ 的圆面积，即 $A$ 的面积 $=\frac{3}{4}\times {{40}^{2}}-\frac{2}{4}\left( \text{}\!\!\pi\!\!\text{ }{{20}^{2}} \right)=200\left( 6-\text{ }\!\!\pi\!\!\text{ }\right)\approx 571.7$，故所求的结果为572．
也就是说试题中所述的区域应在以 $\left(20, 0 \right)$ 为圆心，以20为半径的圆的外部，同时也在以 $\left( 0, 20 \right)$ 为圆心以20为半径的圆的外部；即在图中阴影标出的部分．按图中所示，$A$ 的面积为总面积的 $\frac{3}{4}$（总面积减去图中虚线所示的小正方形的面积）减去两个 $\frac{1}{4}$ 的圆面积，即 $A$ 的面积 $=\frac{3}{4}\times {{40}^{2}}-\frac{2}{4}\left( \text{}\!\!\pi\!\!\text{ }{{20}^{2}} \right)=200\left( 6-\text{ }\!\!\pi\!\!\text{ }\right)\approx 571.7$，故所求的结果为572．
答案
解析
备注
