在三角形 $ABC$ 中，$AB=9$，$BC:CA=40:41$．这个三角形面积的最大值是多少？
【难度】
【出处】
1992年第10届美国数学邀请赛（AIME）
【标注】
【答案】
820
【解析】
如图所示，设 $AB=c$，$AC=br$，$BC=ar$；这里 $a<b$．我们将证明 $C$ 点的轨迹是一个中心在直线 $AB$ 上，半径是 $\frac{abc}{{{b}^{2}}-{{a}^{2}}}$ 的圆．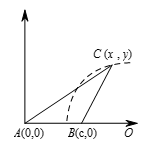
以 $A$ 点为原点，$AB$ 所在直线为横轴建立直角坐标系（如图），设 $A=\left( 0, 0 \right)$，$B=\left( c, 0\right)$，$C=\left( x ,y \right)$．则 $\frac{BC}{AC}=\frac{a}{b}$ 即有 $\frac{\sqrt{{{\left(x-c \right)}^{2}}+{{y}^{2}}}}{\sqrt{{{x}^{2}}+{{y}^{2}}}}=\frac{a}{b}$．
两边取平方再作项的调整可得 $\left({{b}^{2}}-{{a}^{2}} \right){{x}^{2}}-2{{b}^{2}}cx+\left( {{b}^{2}}-{{a}^{2}}\right){{y}^{2}}=-{{b}^{2}}{{c}^{2}}$，
配方后得 ${{\left(x-\frac{{{b}^{2}}c}{{{b}^{2}}-{{a}^{2}}}\right)}^{2}}+{{y}^{2}}=\frac{{{a}^{2}}{{b}^{2}}{{c}^{2}}}{{{\left({{b}^{2}}-{{a}^{2}} \right)}^{2}}}$．
因此所有满足试题条件的顶点 $C$ 的轨迹为中心是 $O=\left(\frac{{{b}^{2}}c}{{{b}^{2}}-{{a}^{2}}} ,0 \right)$，半径为 $\frac{abc}{{{b}^{2}}-{{a}^{2}}}$ 的圆．
当此圆的半径成为三角形的高时，此三角形的面积即为最大，故所求最大面积是 $\frac{1}{2}c\left( \frac{abc}{{{b}^{2}}-{{a}^{2}}} \right)$．
当 $a:b=40:41$ 而 $c=9$ 时，可得答案820．
以 $A$ 点为原点，$AB$ 所在直线为横轴建立直角坐标系（如图），设 $A=\left( 0, 0 \right)$，$B=\left( c, 0\right)$，$C=\left( x ,y \right)$．则 $\frac{BC}{AC}=\frac{a}{b}$ 即有 $\frac{\sqrt{{{\left(x-c \right)}^{2}}+{{y}^{2}}}}{\sqrt{{{x}^{2}}+{{y}^{2}}}}=\frac{a}{b}$．两边取平方再作项的调整可得 $\left({{b}^{2}}-{{a}^{2}} \right){{x}^{2}}-2{{b}^{2}}cx+\left( {{b}^{2}}-{{a}^{2}}\right){{y}^{2}}=-{{b}^{2}}{{c}^{2}}$，
配方后得 ${{\left(x-\frac{{{b}^{2}}c}{{{b}^{2}}-{{a}^{2}}}\right)}^{2}}+{{y}^{2}}=\frac{{{a}^{2}}{{b}^{2}}{{c}^{2}}}{{{\left({{b}^{2}}-{{a}^{2}} \right)}^{2}}}$．
因此所有满足试题条件的顶点 $C$ 的轨迹为中心是 $O=\left(\frac{{{b}^{2}}c}{{{b}^{2}}-{{a}^{2}}} ,0 \right)$，半径为 $\frac{abc}{{{b}^{2}}-{{a}^{2}}}$ 的圆．
当此圆的半径成为三角形的高时，此三角形的面积即为最大，故所求最大面积是 $\frac{1}{2}c\left( \frac{abc}{{{b}^{2}}-{{a}^{2}}} \right)$．
当 $a:b=40:41$ 而 $c=9$ 时，可得答案820．
答案
解析
备注
