在三角形 $ABC$ 中，${A}'$，${B}'$ 和 ${C}'$ 分别在 $BC$，$AC$ 和 $AB$ 上，$A{A}'$，$B{B}'$ 和 $C{C}'$ 相交于一点 $O$，并且 $\frac{AO}{O{A}'}+\frac{BO}{O{B}'}+\frac{CO}{O{C}'}=92$，求 $\frac{AO}{O{A}'}\cdot \frac{BO}{O{B}'}\cdot \frac{CO}{O{C}'}$ 的值．
【难度】
【出处】
1992年第10届美国数学邀请赛（AIME）
【标注】
【答案】
94
【解析】
如图所示，因 $\vartriangle AOB$ 和 $\vartriangle {A}'OB$ 有相同的高度，同样，$\vartriangle AOC$ 和 $\vartriangle {A}'OC$ 也有相同的高度，
故 $\frac{AO}{O{A}'}=\frac{{{S}_{\vartriangle AOB}}}{{{S}_{\vartriangle {A}'OB}}}=\frac{{{S}_{\vartriangle COA}}}{{{S}_{\vartriangle CO{A}'}}}=\frac{{{S}_{\vartriangle AOB}}+{{S}_{\vartriangle COA}}}{{{S}_{\vartriangle {A}'OB}}+{{S}_{\vartriangle CO{A}'}}}$
$=\frac{{{S}_{\vartriangle AOB}}+{{S}_{\vartriangle COA}}}{{{S}_{\vartriangle BOC}}}=\frac{z+y}{x}$，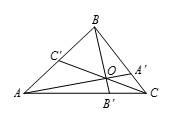
这里 $x={{S}_{\vartriangle BOC}}$，$y={{S}_{\vartriangle COA}}$，$z={{S}_{\vartriangle AOB}}$．类似地，可得 $\frac{BO}{O{B}'}=\frac{x+y}{z}$，$\frac{CO}{O{C}'}=\frac{x+y}{z}$．
从而有 $\frac{AO}{O{A}'}\cdot\frac{BO}{O{B}'}\cdot \frac{CO}{O{C}'}=\frac{\left( z+y \right)\left( x+z\right)\left( y+x \right)}{xyz}$
$=\frac{y{{z}^{2}}+{{y}^{2}}z+{{x}^{2}}z+x{{z}^{2}}+x{{y}^{2}}+{{x}^{2}}y+2xyz}{xyz}$
$=\frac{yz\left( z+y \right)+xz\left( x+z\right)+xy\left( y+x \right)}{xyz}+2$
$=\frac{z+y}{x}+\frac{x+z}{y}+\frac{y+x}{z}+2$．
因此 $\frac{AO}{O{A}'}\cdot\frac{BO}{O{B}'}\cdot \frac{CO}{O{C}'}=\left(\frac{AO}{O{A}'}+\frac{BO}{O{B}'}+\frac{CO}{O{C}'} \right)+2=92+2=94$．
故 $\frac{AO}{O{A}'}=\frac{{{S}_{\vartriangle AOB}}}{{{S}_{\vartriangle {A}'OB}}}=\frac{{{S}_{\vartriangle COA}}}{{{S}_{\vartriangle CO{A}'}}}=\frac{{{S}_{\vartriangle AOB}}+{{S}_{\vartriangle COA}}}{{{S}_{\vartriangle {A}'OB}}+{{S}_{\vartriangle CO{A}'}}}$
$=\frac{{{S}_{\vartriangle AOB}}+{{S}_{\vartriangle COA}}}{{{S}_{\vartriangle BOC}}}=\frac{z+y}{x}$，
这里 $x={{S}_{\vartriangle BOC}}$，$y={{S}_{\vartriangle COA}}$，$z={{S}_{\vartriangle AOB}}$．类似地，可得 $\frac{BO}{O{B}'}=\frac{x+y}{z}$，$\frac{CO}{O{C}'}=\frac{x+y}{z}$．从而有 $\frac{AO}{O{A}'}\cdot\frac{BO}{O{B}'}\cdot \frac{CO}{O{C}'}=\frac{\left( z+y \right)\left( x+z\right)\left( y+x \right)}{xyz}$
$=\frac{y{{z}^{2}}+{{y}^{2}}z+{{x}^{2}}z+x{{z}^{2}}+x{{y}^{2}}+{{x}^{2}}y+2xyz}{xyz}$
$=\frac{yz\left( z+y \right)+xz\left( x+z\right)+xy\left( y+x \right)}{xyz}+2$
$=\frac{z+y}{x}+\frac{x+z}{y}+\frac{y+x}{z}+2$．
因此 $\frac{AO}{O{A}'}\cdot\frac{BO}{O{B}'}\cdot \frac{CO}{O{C}'}=\left(\frac{AO}{O{A}'}+\frac{BO}{O{B}'}+\frac{CO}{O{C}'} \right)+2=92+2=94$．
答案
解析
备注
