在Chomp游戏中,两人轮流从 $5\times 7$ 个方格拼成的矩形板上拿取方格,每次从剩余的方格中选择一个方格,且“吃掉”(拿掉)它,同时由这个方格的左边(向上方的延长线)和下边(向右边的延长线)限定的范围内的所有方格也将一起被“吃掉”.例如,当拿掉图中阴影方格时,四个带有“$\times $”的方格也将拿掉(那些由两条或两条以上虚线所确定的方格在这之前已被拿掉了).游戏的目标是迫使对方去“吃掉”最后一个方格.以方格为元素组成一个 $5\times 7$ 的方格集合,游戏进行中的每一步所剩下的方格是这个集合的一个子集,图中所示的方格集(除去有虚线为边的方格)便是游戏过程中众多子集中的一个.那么这样的子集共有多少个,包括整个矩形($5\times 7$ 个方格全体)和空板(空集)在内?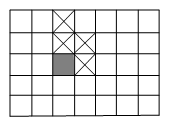

【难度】
【出处】
1992年第10届美国数学邀请赛(AIME)
【标注】
【答案】
792
【解析】
该游戏进行过程的每一步结束后,未被“吃掉”的小方格组成之图形有如下特点:当从左至右考查时,由单个小方格摞起来的立柱之高度是非增加的,不难证明这一特点不仅是必要的,也是充分的,也就是说,如果小方格组成的图形具有这一特点,它一定是某个游戏过程中某一步后的结果(读者应证明这一事实).进而言之,每一个这样的图形都可完全地由12个边组成的折线描绘出来,该折线由原始图形(全板)左边最上端的小方格之一边起延续到右边最下端的小方格之一边止,每一边都是被“吃掉”的和未被“吃掉”的小方格的公共边界.这些边界可用由V和H两个字母组成的12字序列表示出来,该序列中含有7个H和5个V,其中H表示未被“吃掉”的立柱的顶部(或已被“吃掉”的立柱的底部)那一段边;V表示某个小方格的垂直边,该边从未被“吃掉”的立柱顶部起到与之相邻的较短的立柱顶部止.例如,题图中“吃掉”虚线部分以后所剩下的图形可描述为HHHVHVVHHHVV,如图中所示图形可表示为VVHHHHVHVVHH.7个H和5个V所组成的序列共有 $\frac{12!}{7!5!}=792$ 种,其中包括HHHHHHHVVVVV和VVVVVHHHHHHH,即全板(原始图形)和空板.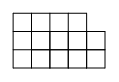

答案
解析
备注