在梯形 $ABCD$ 中，$AB=92$，$BC=50$，$CD=19$，$AD=70$，$AB$ 平行于 $CD$，以 $AB$ 上的点 $P$ 为圆心的圆与 $BC$ 和 $AD$ 相切．已知 $AP=\frac{m}{n}$，其中 $m$ 和 $n$ 是互素的正整数，求 $m+n$．
【难度】
【出处】
1992年第10届美国数学邀请赛（AIME）
【标注】
【答案】
164
【解析】
如图所示，延长 $AD$ 和 $BC$ 相交于 $Q$．因点 $P$ 到 $AQ$ 和 $BQ$ 之距离相等，故点 $P$ 也在 $\angle AQB$ 之角等分线上，因三角形某角之角平分线分该角所对边为两部分，这两部分长之比等于与其连接的两边长度之比，故 $\frac{AP}{BP}=\frac{AQ}{BQ}$．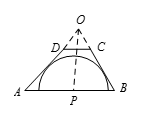
又由于 $AB\parallel CD$，则有 $\frac{AQ}{BQ}=\frac{AD}{BC}=\frac{7}{5}$．
从而 $\frac{AP}{BP}=\frac{7}{5}$，又因 $AP+PB=92$，所以 $AP=\frac{161}{3}$，故 $m+n=164$．
又由于 $AB\parallel CD$，则有 $\frac{AQ}{BQ}=\frac{AD}{BC}=\frac{7}{5}$．从而 $\frac{AP}{BP}=\frac{7}{5}$，又因 $AP+PB=92$，所以 $AP=\frac{161}{3}$，故 $m+n=164$．
答案
解析
备注
