重置
序号 ID 年级 类型 来源 摘要 创建时间
17164 5e5c70aa210b280d378223f8 高中 解答题 高考真题 $2019$ 年，我国施行个人所得税专项附加扣除办法，涉及子女教育，继续教育，大病医疗，住房贷款利息或者住房佣金，赡养老人等六项专项附加扣除．某单位老，中，青员工分别有 $72,108,120$ 人，现采用分层抽样的方法，从该单位上述员工中抽取 $25$ 人调查专项附加扣除的享受情况．
（I）应从老，中，青员工中分别抽取多少人？
（II）抽取的 $25$ 人中，享受至少两项专项附加扣除的员工有 $6$ 人，分别记为 $A,B,C,D,E,F$，享受情况如右表，其中“$\bigcirc$”表示享受，“$\times$”表示不享受．现从这 $6$ 个人中随机抽取 $2$ 人接受采访．\[\begin{array}{|c|c|c|c|c|c|c|}\hline \text{项目\员工}&A&B&C&D&E&F\\\hline \text{子女教育}&\bigcirc&\bigcirc&\times&\bigcirc&\times&\bigcirc\\\hline \text{继续教育}&\times&\times&\bigcirc&\times&\bigcirc&\bigcirc\\\hline \text{大病医疗}&\times&\times&\times&\bigcirc&\times&\times\\\hline
\text{住房贷款利息}&\bigcirc&\bigcirc&\times&\times&\bigcirc&\bigcirc\\\hline \text{住房租金}&\times&\times&\bigcirc&\times&\times&\times\\\hline \text{赡养老人}&\bigcirc&\bigcirc&\times&\times&\times&\bigcirc\\\hline\end{array}\]（i）试用所给字母列举出所有可能的抽取结果；
（ii）设 $M$ 为事件“抽取的 $2$ 人享受的专项附加扣除至少有一项相同”，求事件 $M$ 发生的概率．		 2022-04-17 19:48:29
17151 5e548633210b280d361114c3 高中 解答题 高考真题 设甲，乙两位同学上学期间，每天 $7:30$ 之前到校的概率均为 $\dfrac{2}{3}$．假定甲，乙两位同学到校情况互不影响，且任一同学每天到校情况相互独立．
（I）用 $X$ 表示甲同学上学期间的三天中 $7:30$ 之前到校的天数，求随机变量 $X$ 的分布列和数学期望．
（II）设 $M$ 为事件“上学期间的三天中，甲同学在 $7:30$ 之前到校的天数比乙同学在 $7:30$ 之前到校的天数恰好多 $2$”，求事件 $M$ 发生的概率．		 2022-04-17 19:41:29
17144 5e4f4e5c210b280d36111426 高中 解答题 高考真题 改革开放以来，人们的支付方式发生了巨大改变．近年来，移动支付已成为主要支付方式之一．为了解某校学生上个月 $A,B$ 两种移动支付方式的使用情况，从全校所有的 $1000$ 学生中随机抽取了 $100$ 人，发现样本中 $A,B$ 两种支付方式都不使用的有 $5$ 人，样本中仅使用 $A$ 和仅使用 $B$ 的学生的支付金额分布情况如下：\[\begin{array}{|c|c|c|}\hline\text{支付方式\支付金额(元)}&\text{不大于}2000\text{元}&\text{大于}2000\text{元}\\\hline\text{仅使用}A&27\text{人}&3\text{人}\\\hline\text{仅使用}B&24\text{人}&1\text{人}\\\hline\end{array}\]（I）估计该学生上个月 $A,B$ 两种支付方式都使用的人数；
（II）从样本仅使用 $B$ 的学生中随机抽取 $1$ 人，求该学生上个月支付金额大于 $2000$ 元的概率；
（III）已知上个月样本学生的支付方式在本月没有变化．现从样本仅使用 $B$ 的学生中，随机抽查 $1$ 人，发现他本月的支付金额都大于 $2000$ 元．结合（II）的结果，能否认为样本仅使用 $B$ 的学生中本月支付金额大于 $2000$ 元的人数有变化？说明理由．		 2022-04-17 19:37:29
17123 5e4b7a79210b280d3611126d 高中 解答题 高考真题 设 $(1+x)^n=a_0+a_1x+a_2x^2+\cdots+a_nx^n$．已知 $a_3^2=2a_2a_4$．
（1）求 $n$ 的值；（2）设 $(1+\sqrt{3})^n=a+b\sqrt{3}$，其中 $a,b\in\mathbb{N}^{\ast}$，求 $a^2-3b^2$ 的值．		 2022-04-17 19:26:29
17122 5e4b7b18210b280d37822111 高中 解答题 高考真题 在平面直角坐标系 $xOy$ 中，设点集 $A_n=\{(0,0),(1,0),(2,0),\cdots,(n,0)\},B_n=\{(0,1),(n,1)\}$ $C_n=\{(0,2),(1,2),(2,2),\cdots,(n,2)\}$，
令 $M_n=A_n\bigcup B_n\bigcup C_n$．从集合 $M_n$ 中任取两个不同的点，用随机变量 $X$ 表示它们之间的距离．
（1）当 $n=1$ 时，求 $X$ 的概率分布；
（2）对给定的正整数 $n(n\geqslant 3)$，求概率 $P(X\leqslant n)$（用 $n$ 表示）．		 2022-04-17 19:25:29
17117 5e44be7f210b280d361110c0 高中 解答题 高考真题 为了治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验．试验方案如下：每一轮选取两只白鼠对药效进行对比试验．对于两只白鼠，随机选一只施以甲药，另一只施以乙药．一轮的治疗结果得出后，再安排下一轮试验．当其中一种药治愈的白鼠比另一种药治愈的白鼠多 $4$ 只时，就停止试验，并认为治愈只数多的药更有效．为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得 $1$ 分，乙药得 $-1$ 分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得 $1$ 分，甲药得 $-1$ 分；若都治愈或都未治愈则两种药均得 $0$ 分．甲、乙两种药的治愈率分别记为 $\alpha$ 和 $\beta$，一轮试验中甲药的得分记为 $X$．
（1）求 $X$ 的分布列；
（2）若甲药、乙药在试验开始时都赋予 $4$ 分，$p_i(i=0,1,\cdots,8)$ 表示“甲药的累计得分为 $i$ 时，最终认为甲药比乙药更有效”的概率，则 $p_0=0,p_8=1,p_i=ap_{i-1}+bp_i+cp_{i+1}(i=1,2,\cdots,7)$，其中 $a=P(X=-1),b=P(X=0),c=P(X=1)$．假设 $\alpha=0.5,\beta=0.8$．
（i）证明：$\{p_{i+1}-p_i\}(i=0,1,2,\cdots,7)$ 为等比数列；
（ii）求 $p_4$，并根据 $p_4$ 的值解释这种试验方案的合理性．		 2022-04-17 19:23:29
17113 5e426a81210b280d3611101d 高中 解答题 高考真题 $11$ 分制乒乓球比赛，每赢一球得 $1$ 分，当某局打成 $10:10$ 平后，每球交换发球权，先多得 $2$ 分的一方获胜，该局比赛结束．甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为 $0.5$，乙发球时甲得分的概率为 $0.4$，各球的结果相互独立．在某局双方 $10:10$ 平后，甲先发球，两人又打了 $X$ 个球该局比赛结束．
（1）求 $P(X=2)$；
（2）求事件“$X=4$ 且甲获胜”的概率．		 2022-04-17 19:20:29
17107 5e3ccda6210b286bd531929a 高中 解答题 高考真题 为了了解甲，乙两种离子在小鼠体内的残留程度，进行如下实验．将 $200$ 只小鼠随机分成 $A,B$ 两组，每组 $100$ 只，其中 $A$ 组小鼠给服甲离子溶液，$B$ 组小鼠给服乙离子溶液，每只小鼠给服的溶液体积相同，摩尔浓度相同．经过一段时间启用某种科学方法测算出残留在小鼠体内离子的百分比，根据实验数据分别得到如下直方图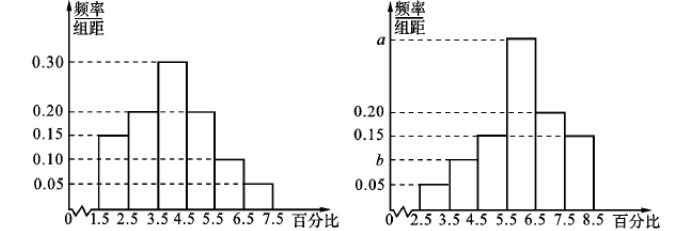：记 $C$ 为事件："乙离子残留在体内的百分比不低于 $5.5$ "，根据直方图得到的 $P(C)$ 的估计值为 $0.70$．
（1）求乙离子残留百分比直方图中 $a,b$ 的值；
（2）分别估计甲，乙离子残留百分比的平均值（同一组中的数据用该组区间的中点值为代表）．		 2022-04-17 19:17:29
17016 599165ca2bfec200011e1c9d 高中 解答题 高考真题 海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了 $100$ 个网箱，测量各箱水产品的产量（单位：$\rm {kg}$），其频率分布直方图如下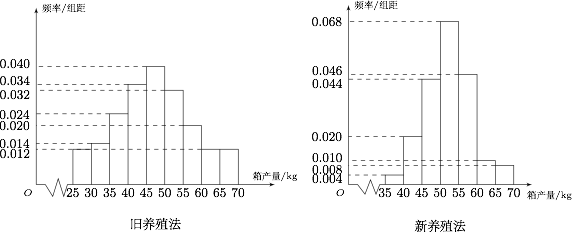：  2022-04-17 19:27:28
17010 599165ca2bfec200011e1c57 高中 解答题 高考真题 某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶 $4$ 元，售价每瓶 $6$ 元，未售出的酸奶降价处理，以每瓶 $2$ 元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：$^{\circ}\mathrm C$）有关．如果最高气温不低于 $25$，需求量为 $500$ 瓶；如果最高气温位于区间 $[20,25)$，需求量为 $300$ 瓶；如果最高气温低于 $20$，需求量为 $200$ 瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：$$\begin{array}{|c|c|c|c|c|c|c|}\hline \mbox{最高气温}&[10,15)&[15,20)&[20,25)&[25,30)&[30,35)&[35,40) \\ \hline \mbox{天数}&2&16&36&25&7&4 \\ \hline \end{array}$$以最高气温位于各区间的频率代替最高气温位于该区间的概率． 2022-04-17 19:24:28
17003 599165ca2bfec200011e1c12 高中 解答题 高考真题 为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取 $16$ 个零件，并测量其尺寸（单位：$\rm cm$）．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布 $N(\mu,\sigma^2)$． 2022-04-17 19:17:28
16997 599165ca2bfec200011e1b45 高中 解答题 高考真题 在心理研究中，常采用对比试验的方法评价不同心理暗示对人的影响，具体方法如下：将参加试验的志愿者随机分成两组，一组接受甲种心理暗示，另一组接受乙种心理暗示，通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用．现有 $6$ 名男志愿者 $A_{1},A_{2},A_{3},A_{4},A_{5},A_{6}$ 和 $4$ 名女志愿者 $B_{1},B_{2},B_{3},B_{4}$，从中随机抽取 $5$ 人接受甲种心理暗示，另 $5$ 人接受乙种心理暗示． 2022-04-17 19:13:28
16981 599165ca2bfec200011e1afe 高中 解答题 高考真题 已知一个口袋中有 $m$ 个白球，$n$ 个黑球（$m,n\in \mathbb N^*$，$n\geqslant 2$），这些球除颜色外完全相同．现将口袋中的球随机地逐个取出，并放入如图所示的编号为 $1,2,3,\cdots,m+n$ 的抽屉内，其中第 $k$ 次取出的球放入编号为 $k$ 的抽屉（$k=1,2,3,\cdots,m+n$．）$$\begin{array}{|c|c|c|c|c|}\hline
1 &2&3&\cdots&m+n \\ \hline
\end{array}$$		 2022-04-17 19:05:28
16974 599165c92bfec200011e19f1 高中 解答题 高考真题 从甲地到乙地要经过 $3$ 个十字路口，设各路口信号灯工作相互独立，且在各路口遇到红灯的概率分别为 $\dfrac12,\dfrac13,\dfrac14$． 2022-04-17 19:00:28
16966 599165c92bfec200011e19b5 高中 解答题 高考真题 为了研究一种新药的疗效，选 $100$ 名患者随机分成两组，每组各 $50$ 名，一组服药，另一组不服药．一段时间后，记录了两组患者的生理指标 $x$ 和 $y$ 的数据，并制成下图，其中“$\ast$ *”表示服药者，“$+$”表示未服药者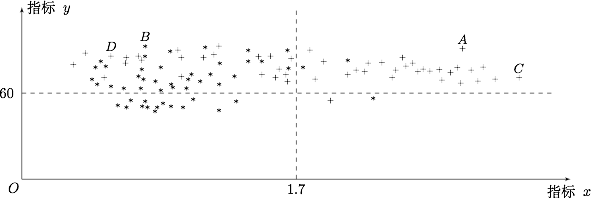． 2022-04-17 19:56:27
16934 599165c92bfec200011e1831 高中 解答题 高考真题 甲、乙两人组成“星队”参加猜成语活动，每轮活动由甲、乙各猜一个成语，在一轮活动中，如果两人都猜对，则“星队”得 $3$ 分；如果只有一人猜对，则“星队”得 $1$ 分；如果两人都没猜对，则“星队”得 $0$ 分．已知甲每轮猜对的概率是 $\dfrac{3}{4}$，乙每轮猜对的概率是 $\dfrac{2}{3}$；每轮活动中甲、乙猜对与否互不影响，各轮结果亦互不影响．假设“星队”参加两轮活动，求： 2022-04-17 19:37:27
16932 599165c92bfec200011e17b1 高中 解答题 高考真题 某小组共 $10$ 人，利用假期参加义工活动，已知参加义工活动次数为 $1$，$2$，$3$ 的人数分别为 $3$，$3$，$4$，现从这 $10$ 人中随机选出 $2$ 人作为该组代表参加座谈会． 2022-04-17 19:37:27
16929 599165c82bfec200011e1734 高中 解答题 高考真题 我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准 $x$（吨），一位居民的月用水量不超过 $x$ 的部分按平价收费，超出 $x$ 的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年 $100$ 位居民每人的月均用水量（单位：吨），将数据按照 $\left[0,0.5\right),\left[0.5,1\right),\cdots,\left[4,4.5\right)$ 分成 $9$ 组，制成了如图所示的频率分布直方图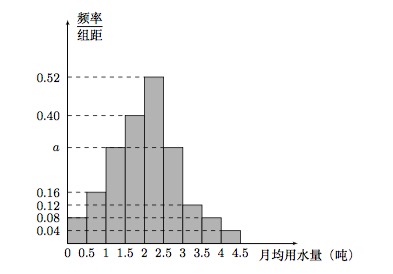．  2022-04-17 19:35:27
16924 599165c82bfec200011e16b7 高中 解答题 高考真题 $A$、$B$、$C$ 三个班共有 $100$ 名学生，为调查他们的体育锻炼情况，通过分层抽样获得了部分学生一周的锻炼时间，数据如下表（单位：小时）：\[\begin{array}{|c|cccccccc|} \hline
A班 & 6& 6.5&7&7.5&8 \\\hline
B班&6&7&8&9&10&11&12 \\\hline
C班&3&4.5&6&7.5&9&10.5&12&13.5\\\hline
\end{array}\]		 2022-04-17 19:32:27
16921 599165c82bfec200011e1633 高中 解答题 高考真题 某险种的基本保费为 $a$（单位：元），继续购买该险种的投保人称为续保人，续保人本年度的保费与其上年度出险次数的关联如下：\[\begin{array}{|c|c|c|c|c|c|c|}\hline { 上年度出险次数 }&0&1&2&3&4&{\geqslant 5}\\ \hline { 保费 }&{0.85a}&a&{1.25a}&{1.5a}&{1.75a}&{2a}\\ \hline\end{array}\]设该险种一续保人一年内出险次数与相应概率如下：\[\begin{array}{|c|c|c|c|c|c|c|}\hline{ 一年内出险次数 }&0&1&2&3&4&{\geqslant 5}\\ \hline { 概率 }&{0.30}&{0.15}&{0.20}&{0.20}&{0.10}&{0.05}\\ \hline\end{array}\] 2022-04-17 19:31:27
0.174441s