我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准 $x$(吨),一位居民的月用水量不超过 $x$ 的部分按平价收费,超出 $x$ 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年 $100$ 位居民每人的月均用水量(单位:吨),将数据按照 $\left[0,0.5\right),\left[0.5,1\right),\cdots,\left[4,4.5\right)$ 分成 $9$ 组,制成了如图所示的频率分布直方图.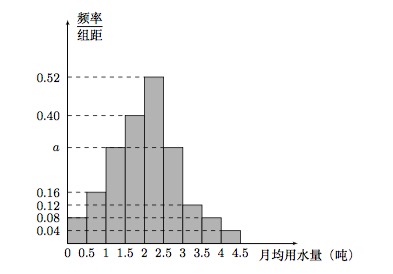

【难度】
【出处】
2016年高考四川卷(理)
【标注】
-
求直方图中 $a$ 的值;标注答案$a=0.3$解析本题考查频率分布直方图中小矩形的面积之和为 $1$.由概率统计相关知识,各组频率之和的值为 $1$,所以\[0.5\cdot \left( 0.08+0.16+0.4+0.52+0.12+0.08+0.04+2a \right)=1,\]解得 $a=0.3$.
-
设该市有 $30$ 万居民,估计全市居民中月均用水量不低于 $3$ 吨的人数,并说明理由;标注答案$3.6$ 万解析本题考查用样本估计总体,计算出对应的样本的数字特征即可估计总体的.由图,不低于 $3$ 吨的人数所占百分比为\[0.5\cdot \left( 0.12+0.08+0.04 \right) = 12\%,\]故全市月均用水量不低于 $3$ 吨的人数为 $30\cdot 12\%=3.6$(万).
-
若该市政府希望使 $85\%$ 的居民每月的用水量不超过标准 $x$(吨),估计 $x$ 的值,并说明理由.标注答案$2.9$ 吨解析本题考查从频率分布直方图中找出对应频率的数值的方法.首先确定出对应频率的数值所在的区间,然后根据比例具体计算即可.由图可知,月均用水量小于 $2.5$ 吨的居民人数所占百分比为\[0.5\cdot \left( 0.08+0.16+0.3+0.4+0.52 \right)=0.73,\]即 $73\%$ 的居民月均用水量小于 $2.5$ 吨,同理,$88\%$ 的居民月均用水量小于 $3$ 吨,故 $2.5<x<3$.
假设月均用水量平均分布,则$x=2.5+0.5\cdot \dfrac{\left( 85\%-73\% \right)\div 0.5}{0.3}=2.9$(吨).
注:本次估计默认组间是平均分布,与实际可能会产生一定误差.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3