海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了 $100$ 个网箱,测量各箱水产品的产量(单位:$\rm {kg}$),其频率分布直方图如下: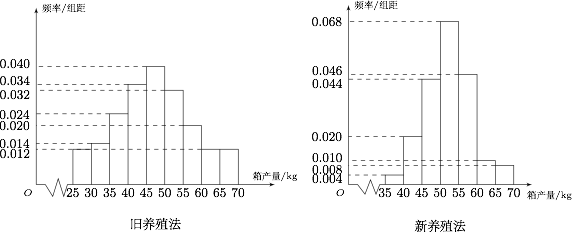

【难度】
【出处】
2017年高考全国甲卷(理)
【标注】
-
设两种养殖方法的箱产量互相独立,记 $A$ 表示事件“旧养殖法的箱产量低于 $50{\rm {kg}}$,新养殖法的箱产量不低于 $50{\rm{kg}}$”,估计 $A$ 的概率;标注答案$0.4092$解析记 $B$ 表示事件“旧养殖法的箱产量低于 $50{\rm {kg}}$”,$C$ 表示事件“新养殖法的箱产量不低于 $50\rm{kg}$”.
由题意知 $P(A)=P(BC)=P(B)P(C)$.旧养殖法的箱产量低于 $50\rm {kg}$ 的频率为\[(0,012+0.014+0.024+0.034+0.040)\times 5=0.62.\]故 $P(B)$ 的估计值为 $0.66$.因此,事件 $A$ 的概率估计值为 $0.62\times 0.66 =0.4092$. -
填写下面列联表,并根据列联表判断是否有 $99\%$ 的把握认为箱产量与养殖方法有关:\[\begin{array}{|c|c|c|}\hline \quad&\mbox{箱产量}<50{\rm {kg}}&\mbox{箱产量}\geqslant 50{\rm {kg}}\\ \hline\mbox{旧养殖法}&&\\ \hline\mbox{新养殖法}&&\\ \hline\end{array}\]附:$\begin{array}{c|ccc} P(K^{2}\geqslant k)&0.050&0.010&0.001\\ \hline k&3.841&6.635&10.828\end{array}$,$K^{2}=\dfrac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.标注答案$\begin{array}{|c|c|c|}\hline &\text{箱产量}<50{\rm {kg}}& \text{箱产量}\geqslant 50{\rm {kg}}\\ \hline \text{旧养殖法}&62&38\\ \hline \text{新养殖法}&34&66\\ \hline \end{array}$,有 $99\%$ 的把握认为箱产量与养殖方法有关解析根据箱产量的频率分布直方图得到列联表\[\begin{array}{|c|c|c|}\hline &\text{箱产量}<50{\rm {kg}}& \text{箱产量}\geqslant 50{\rm {kg}}\\ \hline \text{旧养殖法}&62&38\\ \hline \text{新养殖法}&34&66\\ \hline \end{array}\]则 $K^{2}=\dfrac{200\times (61\times 66-34\times 38)^{2}}{100\times 100\times 96\times 104}\approx 15.705>6.635$.所以由 $99\%$ 的把握认为箱产量与养殖方法有关.
-
根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到 $0.01$).标注答案$52.35$解析因为新养殖法的箱产量频率分布直方图中,箱产量低于 $50{\rm {kg}}$ 的直方图面积为\[(0.004+0.020+0.044)\times 5=0.68>0.5,\]故新养殖法箱产量的中位数的估计值为\[50+\dfrac{0.5-0.34}{0.068}\approx 52.35(\rm{kg}).\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3