为了研究一种新药的疗效,选 $100$ 名患者随机分成两组,每组各 $50$ 名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标 $x$ 和 $y$ 的数据,并制成下图,其中“$\ast$ *”表示服药者,“$+$”表示未服药者.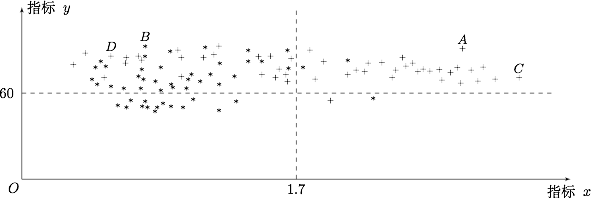

【难度】
【出处】
2017年高考北京卷(理)
【标注】
-
从服药的 $50$ 名患者中随机选出一人,求此人指标 $y$ 的值小于 $60$ 的概率;标注答案$\dfrac 3{10}$解析由图可知 $50$ 名服药者中指标 $y$ 的值小于 $60$ 的人有 $15$ 人,故随机抽取 $1$ 人,此人的指标 $y$ 的值小于 $60$ 的概率为 $\dfrac{15}{50}=\dfrac 3{10}$.
-
从图中 $A,B,C,D$ 四人中随机选出两人,记 $\xi$ 为选出的两人中指标 $x$ 的值大于 $1.7$ 的人数,求 $\xi$ 的分布列和数学期望 $E(\xi)$标注答案$\xi$ 的分布列为\[\begin{array}{|c|c|c|c|}\hline
\xi &0&1&2\\ \hline
P&\dfrac 16 &\dfrac 23 &\dfrac 16\\ \hline\end{array}\]$E(\xi)=1$解析$\xi$ 的可能取值为:$0,1,2$.\[\begin{split}&P(\xi=0)=\dfrac{{\rm C}_2^2}{{\rm C}_4^2}=\dfrac 16,\\ &P(\xi=1)=\dfrac{{\rm C}_2^1\cdot {\rm C}_2^1}{{\rm C}_4^2}=\dfrac 23,\\ &P(\xi=2)=\dfrac{{\rm C}_2^2}{{\rm C}_4^2}=\dfrac 16.\end{split}\]所以 $\xi$ 的分布列为\[\begin{array}{|c|c|c|c|}\hline
\xi &0&1&2\\ \hline
P&\dfrac 16 &\dfrac 23 &\dfrac 16\\ \hline\end{array}\]所以$$E(\xi)=0\cdot \dfrac 16 +1\cdot \dfrac 23 +2\cdot \dfrac 16=1.$$ -
试判断这 $100$ 名患者中服药者指标 $y$ 数据的方差与未服药者指标 $y$ 数据的方差的大小.(只需写出结论)标注答案服药的方差大解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3