重置
序号 ID 年级 类型 来源 摘要 创建时间
27159 590fde18857b4200085f866c 高中 解答题 自招竞赛 设 $a$，$b$ 是从集合 $\{1,2,3,4,5\}$ 中随机选取的数． 2022-04-17 21:39:01
27141 590fed22857b42000aca3905 高中 解答题 自招竞赛 将 $4$ 男、$4$ 女 $8$ 位同学随机地分成人数相等的甲、乙两组． 2022-04-17 21:29:01
27120 59101c15857b4200085f8709 高中 解答题 自招竞赛 两名射手轮流向同一目标射击，射手甲和射手乙命中目标的概率都是 $\dfrac{1}{2}$．若射手甲先射，谁先命中目标谁就获胜，试求甲、乙两射手获胜的概率． 2022-04-17 21:18:01
26953 59126ea6e020e70007fbec3f 高中 解答题 自招竞赛 从一个装有三个红球、两个白球的口袋中任取两球放入一个箱子中． 2022-04-17 20:46:59
26920 59127af2e020e7000a798b0b 高中 解答题 自招竞赛 在蒲丰投针试验中，平行线间距为 $a$，针长为 $b$，试求针与线相交概率与 $a$、$b$ 的关系，并求在什么情况下概率是 $\dfrac{1}{\pi}$． 2022-04-17 20:26:59
26754 59681b230303980008983dad 高中 解答题 自招竞赛 正五边形 $ABCDE$ 的对角线 $BE$ 分别与对角线 $AD$，$AC$ 交于点 $F$，$G$，对角线 $BD$ 分别与对角线 $CA$，$CE$ 交于点 $H$，$I$，对角线 $CE$ 与对角线 $AD$ 交于点 $J$，设由图中 $10$ 个点 $A$，$B$，$C$，$D$，$E$，$F$，$G$，$H$，$I$，$J$ 和线段构成的等腰三角形的集合为 $M$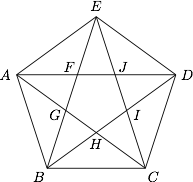． 2022-04-17 20:53:57
26732 5912b15ae020e7000a798c23 高中 解答题 自招竞赛 $12$ 名职员（其中 $3$ 名为男性）被平均分配到 $3$ 个部门． 2022-04-17 20:41:57
26708 5912bd34e020e700094b0d82 高中 解答题 自招竞赛 某厂生产的一批电子元件，按每盒 $10$ 件进行包装，每盒产品均需检验合格后方可出厂，质检办法规定：从每盒 $10$ 件电子元件中任意抽取 $3$ 件进行检验，若次品数不超过 $1$ 件，就认为该盒产品合格；否则就认为该盒产品不合格．已知某盒电子元件中有 $2$ 件次品． 2022-04-17 20:28:57
26684 59141c1e1edfe2000ade9899 高中 解答题 高中习题 “玛丽莲”问题是某电视台娱乐节目“决策”中提出的一系列问题．其中最著名的是“Behind Monty Hall’s Doors”．问题如下：台上有三个关闭的门，一个后边有汽车，其余两个后边是山羊．主持人（Monty Hall）让参加者任意选择其中一个门，然后她打开其余两个门中的一个，参加者看到的是山羊．（注意：主持人事先清楚哪扇门后面是山羊，哪扇门后面是汽车，所以她必然可以保证打开的那扇门后面是山羊）．这时，她让参加者可以重选，也就是说参加者可以换选另一个剩下的门．那么，参加者应该换还是不换？1990年，一位读者把这个问题投寄到《Parade》杂志中一个叫“去问玛丽莲”的专栏中．这个专栏的评论员是以IQ $228$ 而获得吉尼斯智商世界纪录的玛丽莲·佛斯·萨万特．玛丽莲的答案是应该换，但是很多读者不同意．玛丽莲在下一期专栏中给出一个表格说明她的道理，但是反对声更多更大了．在几千封读者来信中，反对者达九成．其中，有全国健康机构的统计学家，国防情报中心的副主任，甚至包括著名的美籍匈牙利数学家Paul Erdos．到底应该换还是不换呢？ 2022-04-17 20:15:57
26655 5975a46c6b07450008983652 高中 解答题 高中习题 已知一个口袋中有 $m$ 个白球，$n$ 个黑球（$m,n\in \mathbb N^*$，$n\geqslant 2$），这些球除颜色外完全相同．现将口袋中的球随机地逐个取出，并放入如图所示的编号为 $1,2,3,\cdots,m+n$ 的抽屉内，其中第 $k$ 次取出的球放入编号为 $k$ 的抽屉（$k=1,2,3,\cdots,m+n$）．\begin{array}{|c|c|c|c|c|}
\hline
1 & 2 & 3 & \cdots & m+n \\
\hline
\end{array}		 2022-04-17 20:00:57
26618 591424251edfe20007c5099e 高中 解答题 高中习题 某常染色体遗传病，基因型为AA的人都患病，Aa的人有 $50\%$ 患病，aa的人都正常．一对新婚夫妇中女性正常，她的母亲患病且基因型为Aa，她的父亲和丈夫的家族中均无该病患者，请推测这对夫妇的子女患该病的概率． 2022-04-17 20:40:56
26239 59706969dbbeff0009d29f10 高中 解答题 高中习题 甲乙等 $4$ 人相互传球，第一次由甲将球传出，每次传球时，传球者将球等可能地传给另外 $3$ 人中的任何 $1$ 人． 2022-04-17 20:09:53
25860 59706a1fdbbeff0009d29f1a 高中 解答题 自招竞赛 将一枚均匀的硬币连续抛掷 $n$ 次，以 ${p_n}$ 表示未出现连续 $3$ 次正面的概率． 2022-04-17 20:48:49
25859 59102a1840fdc7000a51cf53 高中 解答题 高中习题 将一枚均匀的硬币连续抛掷 $n$ 次，以 ${p_n}$ 表示未出现连续 $3$ 次正面的概率． 2022-04-17 20:47:49
25390 5909922538b6b4000adaa26b 高中 解答题 高考真题 随机将 $1,2,\cdots ,2n\left(n \in{\mathbb{N}}^* , n \geqslant 2\right)$ 这 $2n$ 个连续正整数分成 $A$，$B$ 两组，每组 $n$ 个数，$A$ 组最小数为 $a_1$，最大数为 $a_2$；$B$ 组最小数为 $b_1$，最大数为 ${b_2}$，记 $\xi ={a_2}-{a_1}$，$\eta ={b_2}-{b_1}$． 2022-04-17 20:28:45
25350 590fcd53857b420007d3e59c 高中 解答题 自招竞赛 系统中每个元件正常工作的概率都是 $p$（$0 < p < 1$）．各个元件正常工作的时间相互独立．如果系统中有多于一半的元件正常工作，系统就能正常工作．系统正常工作的概率称为系统的可靠性． 2022-04-17 20:04:45
25291 59128910e020e7000878f904 高中 解答题 自招竞赛 甲、乙两人轮流投掷硬币，第一局甲先掷，谁先掷出正面谁就胜，上一局的负者下一局先掷．问： 2022-04-17 20:30:44
24578 5912664ee020e7000a7989c2 高中 解答题 自招竞赛 已知某音响设备由五部分组成，$A$ 电视机，$B$ 影碟机，$C$ 线路，$D$ 左声道，$E$ 右声道，其中每个部件工作的概率如图所示．能听到声音，当且仅当 $A$ 与 $B$ 中有至少一个工作，$C$ 工作，$D$ 与 $E$ 中至少有一工作；且若 $D$ 和 $E$ 同时工作则有立体声效果．
求：		 2022-04-17 20:02:38
24557 591420481edfe2000949ce45 高中 解答题 高中习题 若已知肝癌的发病率是 $0.0004$，并可以通过甲胎蛋白法筛查肝癌．统计表明：用此方法对肝癌病人检验时，$95\%$ 的人呈阳性；而用此方法对非肝癌患者检验时，$90\%$ 的人呈阴性．如果有一个人，他的检验结果呈阳性，那么他患有肝癌的概率是多少？ 2022-04-17 20:50:37
23918 59098ba139f91d000a7e459b 高中 解答题 高中习题 已知袋中有 $10$ 个小球，其中有 $5$ 个红球，$3$ 个黄球，$2$ 个绿球．每次从袋中不放回的取出一个球，问红球首先被全部取出的概率． 2022-04-17 20:54:31
0.166787s