正五边形 $ABCDE$ 的对角线 $BE$ 分别与对角线 $AD$,$AC$ 交于点 $F$,$G$,对角线 $BD$ 分别与对角线 $CA$,$CE$ 交于点 $H$,$I$,对角线 $CE$ 与对角线 $AD$ 交于点 $J$,设由图中 $10$ 个点 $A$,$B$,$C$,$D$,$E$,$F$,$G$,$H$,$I$,$J$ 和线段构成的等腰三角形的集合为 $M$.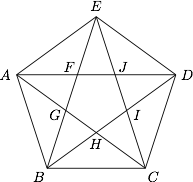

【难度】
【出处】
2010年全国高中数学联赛天津市预赛
【标注】
-
求 $M$ 中元素的个数;标注答案$35$解析因为由图中的 $10$ 个点 $A$,$B$,$C$,$D$,$E$,$F$,$G$,$H$,$I$,$J$ 和线段构成的三角形均为等腰三角形,所以$$|M|=\mathrm C_5^3+4\mathrm C_5^4+5\mathrm C_5^5=35.$$
-
若将这 $10$ 个点中每个点任意染色为红蓝两种颜色之一,问是否一定存在 $M$ 中的一个等腰三角形,其三个顶点同色?标注答案一定存在解析由抽屉原理,$A$,$B$,$C$,$D$,$E$ 中一定有三个点同色,且这三个点构成的三角形属于 $M$.因此一定存在 $M$ 中的一个等腰三角形,其三个顶点同色.
-
若将这 $10$ 个点中的任意 $n$ 个点染为红色,使得一定存在 $M$ 中的一个等腰三角形,其三个顶点同为红色,求 $n$ 的最小值.标注答案$6$解析
情形一 若 $n=5$,将 $F$,$G$,$H$,$I$,$J$ 染为红色,则不存在属于 $M$ 的顶点同为红色的三角形.情形二 若 $n \geqslant 6$,当 $A$,$B$,$C$,$D$,$E$ 中有不少于三个红点时,一定存在属于 $M$ 且顶点同为红色的三角形;当 $A$,$B$,$C$,$D$,$E$ 中少于三个红点时,$F$,$G$,$H$,$I$,$J$ 中至少有 $4$ 个红点.
若 $F$,$G$,$H$,$I$,$J$ 中恰有 $4$ 个红点,不妨假设 $F$,$G$,$H$,$J$ 为红点,则 $A$,$B$,$C$,$D$,$E$ 中至少有两个红点.
若 $A$,$B$,$E$ 中有一个点是红点,不妨假设 $A$ 为红点,则 $\triangle AFG$ 是属于 $M$ 且顶点同为红色的三角形.
否则 $C$,$D$ 同为红色,于是 $\triangle CDH$ 是属于 $M$ 且顶点同为红色的三角形.
若 $F$,$G$,$H$,$I$,$J$ 均为红色,则 $A$,$B$,$C$,$D$,$E$ 中至少有一个点为红色,不妨假设 $A$ 为红色,则 $\triangle AFG$ 属于 $M$ 且顶点同为红色的三角形.
因此 $n$ 的最小值为 $6$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3