重置
序号 ID 年级 类型 来源 摘要 创建时间
27591 59367750c2b4e7000a085454 高中 解答题 高考真题 如图，$O$ 为坐标原点，椭圆 ${C_1}:\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2}= 1$（$a > b > 0$）的左、右焦点分别为 ${F_1},{F_2}$，离心率为 ${e_1}$；双曲线 ${C_2}:\dfrac{x^2}{a^2}- \dfrac{y^2}{b^2}= 1$ 的左、右焦点分别为 ${F_3},{F_4}$，离心率为 ${e_2}$．已知 ${e_1}{e_2}= \dfrac{\sqrt 3}{2}$，且 $\left|{{F_2}{F_4}}\right| = \sqrt 3 - 1$． 2022-04-17 21:42:05
27520 59094970060a05000970b35b 高中 解答题 自招竞赛 一条直线与双曲线交于 $A,B$ 两点，与此双曲线的渐近线交于 $C,D$ 两点，证明：线段 $AC$ 与 $BD$ 的长度相等． 2022-04-17 21:03:05
27494 590950aa060a05000b3d1fca 高中 解答题 高中习题 给出计算双曲线 $y=mx+\dfrac nx$（$m,n>0$）的半实轴长 $a$，半虚轴长 $b$ 以及离心率 $e$ 的算法． 2022-04-17 21:48:04
27486 59096d7b39f91d0009d4bf86 高中 解答题 高考真题 已知双曲线 $E:\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1\left(a > 0,b > 0\right)$ 的两条渐近线分别为 ${l_1}:y = 2x$，${l_2}:y = - 2x$． 2022-04-17 21:42:04
27459 5909864a39f91d0008f0504e 高中 解答题 高考真题 如图，$O$ 为坐标原点，椭圆 ${C_1}:\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2}= 1$（$a > b > 0$）的左、右焦点分别为 ${F_1},{F_2}$，离心率为 ${e_1}$；双曲线 ${C_2}:\dfrac{x^2}{a^2}- \dfrac{y^2}{b^2}= 1$ 的左、右焦点分别为 ${F_3},{F_4}$，离心率为 ${e_2}$．已知 ${e_1}{e_2}= \dfrac{\sqrt 3}{2}$，且 $\left|{{F_2}{F_4}}\right| = \sqrt 3 - 1$． 2022-04-17 21:26:04
27455 590987b739f91d0007cc9397 高中 解答题 高考真题 如图，$O$ 为坐标原点，双曲线 ${C_1}:\dfrac{x^2}{a_1^2}- \dfrac{y^2}{b_1^2}= 1\left({a_1}> 0,{b_1}> 0\right)$ 和椭圆 ${C_2}:\dfrac{y^2}{a_2^2}+ \dfrac{x^2}{b_2^2}= 1\left({a_2}>{b_2}> 0\right)$ 均过点 $P\left(\dfrac{2\sqrt 3}{3},1\right)$，且以 ${C_1}$ 的两个顶点和 ${C_2}$ 的两个焦点为顶点的四边形是面积为 $2$ 的正方形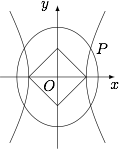． 2022-04-17 21:23:04
27434 590990d838b6b4000adaa25c 高中 解答题 高考真题 如图，已知双曲线 $C:\dfrac{x^2}{a^2}-{y^2}= 1\left(a > 0\right)$ 的右焦点为 $F$．点 $A$，$B$ 分别在 $C$ 的两条渐近线上，$AF \perp x$ 轴，$AB \perp OB$，$BF\parallel OA$（$O$ 为坐标原点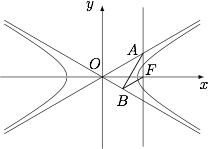）． 2022-04-17 21:13:04
27424 5909ef246cddca00092f6e21 高中 解答题 高中习题 用双曲线的第一定义证明反比例函数 $y=\dfrac{1}{x}$ 的图象是双曲线． 2022-04-17 21:07:04
27423 5909fa176cddca000a08180b 高中 解答题 高中习题 已知过双曲线 $E:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$（$a>b>0$）的焦点 $F$ 的直线被双曲线 $E$ 截得的弦 $AB$ 长为 $l$，根据 $l$ 的大小讨论满足题意的直线条数． 2022-04-17 21:06:04
27392 590aa1a06cddca0008610dc4 高中 解答题 高中习题 已知 $P$ 为双曲线 $H:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ 上的任意一点，双曲线 $H$ 上在点 $P$ 处的切线与双曲线的两条渐近线分别交于 $A,B$ 两点，$O$ 为坐标原点，求 $\triangle AOB$ 外接圆圆心的轨迹方程． 2022-04-17 21:48:03
27166 590fccb7857b4200085f8643 高中 解答题 自招竞赛 已知两点 $A\left( { - 2, 0} \right)$，$B\left( {2, 0} \right)$．动点 $P$ 在 $y$ 轴上的射影是 $H$，且 $\overrightarrow {PA} \cdot \overrightarrow {PB} = 2{\left| {\overrightarrow {PH} } \right|^2}$． 2022-04-17 21:43:01
27156 590fe690857b42000aca38df 高中 解答题 自招竞赛 设双曲线的两个焦点为 $F_1,F_2$，点 $P$ 为双曲线上任意一点．求证：此双曲线在点 $P$ 处的切线平分 $\angle F_1PF_2$． 2022-04-17 21:37:01
27148 590fe8c7857b4200085f8686 高中 解答题 自招竞赛 已知 ${O_1}$ 和 ${O_2}$ 是平面上两个不重合的固定圆周，$C$ 是平面上的一个动圆且与 ${O_1}$、${O_2}$ 都相切．问：$C$ 的圆心轨迹是何种曲线？证明你的结论． 2022-04-17 21:33:01
27085 591029d440fdc70009113dde 高中 解答题 自招竞赛 已知双曲线 $C:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0,b>0)$，点 $F_1,F_2$ 分别为 $C$ 的左右焦点．$P$ 为 $C$ 右支上一点，且使 $\angle F_1PF_2=\dfrac{\pi}{3}$，又 $\triangle {F_1}P{F_2}$ 的面积为 $3\sqrt 3 {a^2}$． 2022-04-17 21:58:00
26994 595afc98866eeb000bce0d15 高中 解答题 高考真题 双曲线 $x^2-\dfrac{y^2}{b^2}=1(b>0) $ 的左、右焦点分别为 $F_1,F_2$，直线 $l$ 过 $F_2$ 且与双曲线交于 $A,B$ 两点． 2022-04-17 21:07:00
26952 59126eeae020e700094b0afc 高中 解答题 自招竞赛 如图，若一倾斜角为 $60^\circ $ 的直线 $l$ 过双曲线 $C$ 的左焦点 $F$ 与双曲线 $C$ 交于 $A,B$ 两点，与双曲线 $C$ 的左准线交于 $M$，若 $\overrightarrow {BM} = \left( {2 + \sqrt 3 } \right)\overrightarrow {AM} $，又 $\left| {\overrightarrow {AB} } \right| = \sqrt 3 $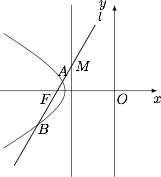． 2022-04-17 20:45:59
26951 59126f26e020e7000878f789 高中 解答题 自招竞赛 过双曲线 $C:{x^2} - \dfrac{{{y^2}}}{3} = {\lambda ^2}$（$\lambda > 0$，$\lambda $ 为常数）的左焦点 $F$ 作斜率为 $k$（$k \ne 0$）的动直线 $l$，$l$ 与双曲线 $C$ 的左、右支分别交于 $A$、$B$ 两点，点 $M$ 满足 $\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} $，其中 $O$ 为坐标原点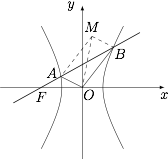． 2022-04-17 20:45:59
26710 5912bbfae020e70007fbee93 高中 解答题 自招竞赛 双曲线 $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$（$a > 0$，$b > 0$）的离心率为 $\sqrt 2 $，$A\left( {{x_1} , {y_1}} \right)$，$B\left( {{x_2} , {y_2}} \right)$ 两点在双曲线上，且 ${x_1} \ne {x_2}$． 2022-04-17 20:29:57
26171 597e9df3d05b9000091651bf 高中 解答题 高中习题 已知 $E$ 是对称轴与坐标轴方向平行或垂直的非圆二次曲线，$A,B,C,D$ 是曲线 $E$ 上的四个不同点，直线 $AC$ 与直线 $BD$ 相交且斜率均存在，求证：$A,B,C,D$ 四点共圆的充要条件是直线 $AC$ 与直线 $BD$ 的斜率互为相反数． 2022-04-17 20:33:52
26163 597e92abd05b90000b5e30c6 高中 解答题 高中习题 已知圆 $O$ 的半径为 $2a$，点 $A$ 在圆 $O$ 外部，且 $|AO|=2c$（$c>a$）．点 $P$ 是圆 $O$ 上的动点，线段 $AP$ 的垂直平分线 $l$ 与直线 $OP$ 相交于点 $M$，求证：$M$ 的轨迹是恒与直线 $l$ 相切的双曲线的一支． 2022-04-17 20:29:52
0.148892s