过双曲线 $C:{x^2} - \dfrac{{{y^2}}}{3} = {\lambda ^2}$($\lambda > 0$,$\lambda $ 为常数)的左焦点 $F$ 作斜率为 $k$($k \ne 0$)的动直线 $l$,$l$ 与双曲线 $C$ 的左、右支分别交于 $A$、$B$ 两点,点 $M$ 满足 $\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} $,其中 $O$ 为坐标原点.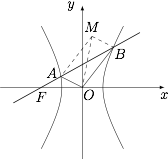

【难度】
【出处】
2007年武汉大学自主招生保送生测试
【标注】
-
求点 $M$ 的轨迹方程;标注答案$3{x^2} + 12\lambda x - {y^2} = 0$($x > 0$)解析双曲线 $C$ 的左焦点为 $F\left( { - 2\lambda , 0} \right)$,所以设$$l:x = my - 2\lambda,m = \dfrac{1}{k}.$$由于双曲线的渐近线为 $y = \pm \sqrt 3 x$,所以 $l$ 与双曲线的左、右支分别相交的充要条件为$$k^2<3,$$即$${m^2} > \dfrac{1}{3}.$$设 $A\left( {{x_1}, {y_1}}\right),B\left( {{x_2}, {y_2}} \right)$,则 点 $M\left( {{x_1} + {x_2}, {y_1} + {y_2}} \right)$ 即为$$M\left( {m\left( {{y_1} + {y_2}} \right) - 4\lambda , {y_1} + {y_2}} \right),$$联立方程,有$$\left( {{m^2} - \dfrac{1}{3}} \right){y^2} - 4m\lambda y + 3{\lambda ^2} = 0,$$所以$${y_1} + {y_2} = \dfrac{{4m\lambda }}{{{m^2} - \dfrac{1}{3}}},$$因此,$M$ 点的坐标满足的方程为$$x = \dfrac{{ \frac{{4\lambda }}{3}}}{{{m^2} - \frac{1}{3}}},y = \dfrac{{4m\lambda }}{{{m^2} - \frac{1}{3}}},$$消参,有 $3{x^2} + 12\lambda x - {y^2} = 0$($x > 0$).
-
是否存在这样的直线 $l$,使得四边形 $OAMB$ 为矩形?若存在,求出直线 $l$ 的斜率 $k$;若不存在,请说明理由.标注答案存在,且 $k = \pm \dfrac{{\sqrt {15} }}{5}$解析四边形 $OAMB$ 为矩形,当且仅当 $\overrightarrow {OA} \perp \overrightarrow {OB} $,即$$\dfrac{{{y_1}}}{{{x_1}}} \cdot \dfrac{{{y_2}}}{{{x_2}}} = - 1,$$联立双曲线与直线,有$${x^2} - \dfrac{{{y^2}}}{3} = {\lambda ^2}{\left( {\dfrac{{my - x}}{{2\lambda }}} \right)^2},$$所以$$1 - \dfrac{1}{3} = {\lambda ^2} \cdot \dfrac{{{m^2} + 1}}{{4{\lambda ^2}}},$$解得$${m^2} = \dfrac{5}{3} > \dfrac{1}{3},$$所以 $k = \pm \sqrt {\dfrac{3}{5}} =\pm \dfrac{{\sqrt {15} }}{5}$ 为所求.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2