已知圆 $O$ 的半径为 $2a$，点 $A$ 在圆 $O$ 外部，且 $|AO|=2c$（$c>a$）．点 $P$ 是圆 $O$ 上的动点，线段 $AP$ 的垂直平分线 $l$ 与直线 $OP$ 相交于点 $M$，求证：$M$ 的轨迹是恒与直线 $l$ 相切的双曲线的一支．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
连接 $MA,MO$．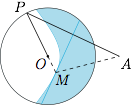
根据题意，有\[|MA|-|MO|=|MP|-|MO|=|OP|=2a,\]于是点 $M$ 的轨迹是以 $O,A$ 为焦点，$2a$ 为实轴长的双曲线 $H$．由于直线 $l$ 与直线 $MO,MA$ 所成的角相等，根据双曲线的光学性质可得直线 $l$ 恒与双曲线 $H$ 相切．
根据题意，有\[|MA|-|MO|=|MP|-|MO|=|OP|=2a,\]于是点 $M$ 的轨迹是以 $O,A$ 为焦点，$2a$ 为实轴长的双曲线 $H$．由于直线 $l$ 与直线 $MO,MA$ 所成的角相等，根据双曲线的光学性质可得直线 $l$ 恒与双曲线 $H$ 相切．
答案
解析
备注
