如图，已知双曲线 $C:\dfrac{x^2}{a^2}-{y^2}= 1\left(a > 0\right)$ 的右焦点为 $F$．点 $A$，$B$ 分别在 $C$ 的两条渐近线上，$AF \perp x$ 轴，$AB \perp OB$，$BF\parallel OA$（$O$ 为坐标原点）．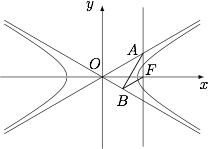
【难度】
【出处】
2014年高考江西卷（理）
【标注】
-
求双曲线 $C$ 的方程；标注答案双曲线 $C$ 的方程为 $\dfrac{x^2}3-y^2=1$解析设直线 $AF$ 与双曲线的另一条渐近线交于点 $E$，则由双曲线的对称性知 $F$ 平分 $AE$，又 $BF\parallel OA$，于是 $B$ 平分 $OE$，而 $AB\perp OB$，因此 $\triangle OAE$ 中，$AO=AE$．又由双曲线的对称性，有 $OA=OE$，因此三角形 $OAE$ 为正三角形，从而有$$\dfrac 1a=\tan\angle AOF=\dfrac{\sqrt 3}3,$$解得 $a=\sqrt 3$，因此双曲线 $C$ 的方程为 $\dfrac{x^2}3-y^2=1$．
-
过 $C$ 上一点 $P\left({x_0},{y_0}\right)\left({y_0}\ne 0\right)$ 的直线 $l:\dfrac{{{x_0}x}}{a^2}-{y_0}y = 1$，与直线 $AF$ 相交于点 $M$，与直线 $x = \dfrac{3}{2}$ 相交于点 $N$．证明：当点 $P$ 在 $C$ 上移动时，$\dfrac{{\left|{MF}\right|}}{{\left|{NF}\right|}}$ 恒为定值，并求此定值．标注答案定值为 $\dfrac{2\sqrt 3}3$解析如图，过 $P$ 作直线 $x=\dfrac 32$ 的垂线，垂足为 $H$，连接 $PF$，$FH$．
由于直线 $l:\dfrac{x_0x}3-y_0y=1$，于是可以解得 $N\left(\dfrac 32,\dfrac{x_0-2}{2y_0}\right)$，因此$$\overrightarrow{FN}\cdot\overrightarrow{FP}=\left(-\dfrac 12,\dfrac{x_0-2}{2y_0}\right)\cdot\left(x_0-2,y_0\right)=0,$$因此 $\angle PFN=\angle PHN=90^\circ$，于是 $P,H,F,N$ 四点共圆，进而$$\angle FPH=\angle FNH=\angle NFM,\angle PFH=\angle PNH=\angle PMF,$$于是 $\triangle PFH$ 与 $\triangle FMN$ 相似，因此$$\dfrac{|MF|}{|NF|}=\dfrac{|PF|}{|PH|}.$$由双曲线的第二定义，$\dfrac{|PF|}{|PH|}$ 为双曲线 $C$ 的离心率 $\dfrac{2}{\sqrt 3}$，因此当点 $P$ 在 $C$ 上移动时，$\dfrac{{\left|{MF}\right|}}{{\left|{NF}\right|}}$ 恒为定值 $\dfrac{2\sqrt 3}3$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
