如图，$O$ 为坐标原点，椭圆 ${C_1}:\dfrac{x^2}{a^2}+ \dfrac{y^2}{b^2}= 1$（$a > b > 0$）的左、右焦点分别为 ${F_1},{F_2}$，离心率为 ${e_1}$；双曲线 ${C_2}:\dfrac{x^2}{a^2}- \dfrac{y^2}{b^2}= 1$ 的左、右焦点分别为 ${F_3},{F_4}$，离心率为 ${e_2}$．已知 ${e_1}{e_2}= \dfrac{\sqrt 3}{2}$，且 $\left|{{F_2}{F_4}}\right| = \sqrt 3 - 1$．
【难度】
【出处】
2014年高考湖南卷（理）
【标注】
-
求 ${C_1},{C_2}$ 的方程；标注答案椭圆 $C_1$ 的方程为 $\dfrac{x^2}2+y^2=1$，双曲线 $C_2$ 的方程为 $\dfrac{x^2}2-y^2=1$解析根据题意，有$$\dfrac{\sqrt{a^2-b^2}}a\cdot\dfrac{\sqrt{a^2+b^2}}a=\dfrac {\sqrt 3}2,\sqrt{a^2+b^2}-\sqrt{a^2-b^2}=\sqrt 3-1,$$解得 $a=\sqrt 2$，$b=1$，因此椭圆 $C_1$ 的方程为 $\dfrac{x^2}2+y^2=1$，双曲线 $C_2$ 的方程为 $\dfrac{x^2}2-y^2=1$．
-
过 ${F_1}$ 作 ${C_1}$ 的不垂直于 $y$ 轴的弦 $AB$，$M$ 为弦 $AB$ 的中点．当直线 $OM$ 与 ${C_2}$ 交于 $P,Q$ 两点时，求四边形 $APBQ$ 面积的最小值．标注答案四边形 $APBQ$ 面积的最小值为 $2$解析如图，作伸缩变换 $\begin{cases} x'=x,\\ y'=\sqrt 2 y,\end{cases}$ 则椭圆变为圆 $x'^2+y'^2=2$，双曲线变为 $x'^2-y'^2=2$．
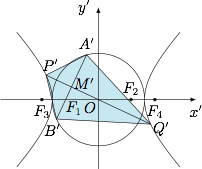此时 $A'B'\perp P'Q'$，因此四边形 $A'P'B'Q'$ 的面积$$S_{A'P'B'Q'}=\dfrac 12|A'B'|\cdot |P'Q'|,$$当 $A'B'\perp x'$ 轴时，线段 $A'B'$ 和线段 $P'Q'$ 的长度同时取得最小值，从而此时 $S_{A'P'B'Q'}$ 最小，为 $\dfrac 12\cdot 2\cdot 2\sqrt 2=2\sqrt 2$．于是四边形 $APBQ$ 面积的最小值为 $\dfrac{1}{\sqrt 2}\cdot 2\sqrt 2=2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
