如图,若一倾斜角为 $60^\circ $ 的直线 $l$ 过双曲线 $C$ 的左焦点 $F$ 与双曲线 $C$ 交于 $A,B$ 两点,与双曲线 $C$ 的左准线交于 $M$,若 $\overrightarrow {BM} = \left( {2 + \sqrt 3 } \right)\overrightarrow {AM} $,又 $\left| {\overrightarrow {AB} } \right| = \sqrt 3 $.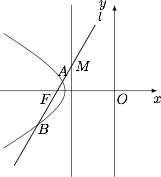

【难度】
【出处】
2007年武汉大学自主招生保送生测试
【标注】
-
求双曲线 $C$ 的离心率;标注答案$\dfrac{{2\sqrt 3 }}{3}$解析设双曲线的方程为 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$,其中 $a>b>0$.其离心率为 $e$,半焦距为 $c$.根据双曲线的焦半径公式 II,有\[\dfrac{AF}{BF}=\dfrac{\dfrac{b^2}{a+c\cos 60^\circ}}{\dfrac{b^2}{a-c\cos 60^\circ}}=\dfrac{1-\dfrac 12e}{1+\dfrac 12e},\]而\[\dfrac{AF}{BF}=\dfrac{AM}{BM}=\dfrac{1}{2+\sqrt 3},\]解得 $e=\dfrac{2\sqrt 3}3$.
-
求双曲线 $C$ 的方程.标注答案$\dfrac{{{x^2}}}{3} - {y^2} = 1$解析根据双曲线的焦点弦长公式,有\[AB=\dfrac{2ab^2}{a^2-c^2\cos^260^\circ}=\dfrac{2a(e^2-1)}{1-\dfrac 14e^2}=a,\]因此 $a=\sqrt 3$,进而 $c=2$,$b=1$,双曲线 $C$ 的方程为 $\dfrac{x^2}3-y^2=1$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2