重置
序号 ID 年级 类型 来源 摘要 创建时间
16456 599165c32bfec200011e05d6 高中 解答题 高考真题 经销商经销某种农产品，在一个销售季度内，每售出 $1 {\mathrm{t}}$ 该产品获利润 $500$ 元，未售出的产品，每 $1 {\mathrm{t}}$ 亏损 $300$ 元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图所示．经销商为下一个销售季度购进了 $130 {\mathrm {t}}$ 该农产品．以 $X$（单位：$ {\mathrm {t}}$，$100 \leqslant X \leqslant 150$）表示下一个销售季度内的市场需求量，$T$（单位：元）表示下一个销售季度内经销该农产品的利润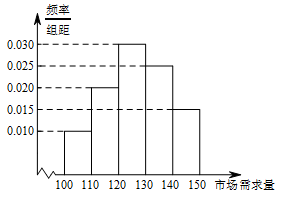．  2022-04-17 19:06:23
16449 599165c22bfec200011e0544 高中 解答题 高考真题 一批产品需要进行质量检验，检验方案是：先从这批产品中任取 $ 4 $ 件作检验，这 $ 4 $ 件产品中优质品的件数记为 $n$．如果 $n = 3$，再从这批产品中任取 $ 4 $ 件作检验，若都为优质品，则这批产品通过检验；如果 $n = 4$，再从这批产品中任取 $ 1 $ 件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．
假设这批产品的优质品率为 $50\% $，即取出的产品是优质品的概率都为 $\dfrac{1}{2}$，且各件产品是否为优质品相互独立．		 2022-04-17 19:01:23
16440 599165c12bfec200011e024f 高中 解答题 高考真题 甲、乙、丙三人进行羽毛球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判．设各局中双方获胜的概率均为 $\dfrac{1}{2}$，各局比赛的结果相互独立，第 $1$ 局甲当裁判． 2022-04-17 19:56:22
16435 599165c12bfec200011e01cd 高中 解答题 高考真题 在一场娱乐晚会上，有 $5$ 位民间歌手（$1$ 至 $5$ 号）登台演唱，由现场数百名观众投票选出最受欢迎歌手．各位观众须彼此独立地在选票上选 $ 3 $ 名歌手，其中观众甲是 $ 1 $ 号歌手的歌迷，他必选 $ 1 $ 号，不选 $ 2 $ 号，另在 $ 3 $ 至 $ 5 $ 号中随机选 $ 2 $ 名．观众乙和丙对 $ 5 $ 位歌手的演唱没有偏爱，因此在 $ 1 $ 至 $ 5 $ 号中随机选 $ 3 $ 名歌手． 2022-04-17 19:53:22
16431 599165c12bfec200011e0187 高中 解答题 高考真题 某商场举行的“三色球”购物摸奖活动规定：在一次摸奖中，摸奖者先从装有 $ 3 $ 个红球与 $ 4 $ 个白球的袋中任意摸出 $ 3 $ 个球，再从装有 $ 1 $ 个蓝球与 $ 2 $ 个白球的袋中任意摸出 $ 1 $ 个球，根据摸出 $ 4 $ 个球中红球与蓝球的个数，设一、二、三等奖如下：\[\begin{array}{|c|c|c|} \hline
奖级 & 摸出红、蓝球个数 & 获奖金额 \\ \hline
一等奖 & 3红1蓝 & 200元 \\ \hline
二等奖 & 3红0蓝 & 50元 \\ \hline
三等奖 & 2红1蓝 & 10元 \\ \hline \end{array}\]其余情况无奖且每次摸奖最多只能获得一个奖级．		 2022-04-17 19:52:22
16425 599165c12bfec200011e00ff 高中 解答题 高考真题 现有 $ 10 $ 道题，其中 $ 6 $ 道甲类题，$ 4 $ 道乙类题，张同学从中任取 $ 3 $ 道题解答． 2022-04-17 19:49:22
16418 599165c12bfec200011e0073 高中 解答题 高考真题 甲、乙两支排球队进行比赛，约定先胜 $ 3 $ 局者获得比赛的胜利，比赛随即结束．除第五局甲队获胜的概率是 $\dfrac{1}{2}$ 外，其余每局比赛甲队获胜的概率都是 $\dfrac{2}{3}$．假设各局比赛结果互相独立． 2022-04-17 19:46:22
16413 599165c12bfec200011e0031 高中 解答题 高考真题 某车间共有 $12$ 名工人，随机抽取 $6$ 名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．\[\begin{array}{c|ccc}1&7&9 \\ 2&0&1&5 \\ 3&0 \end{array} \] 2022-04-17 19:44:22
16408 599165c02bfec200011dff70 高中 解答题 高考真题 下图是某市 $ 3 $ 月 $ 1 $ 日至 $ 14 $ 日的空气质量指数趋势图，空气质量指数小于 $ 100 $ 表示空气质量优良，空气质量指数大于 $ 200 $ 表示空气重度污染．某人随机选择 $ 3 $ 月 $ 1 $ 日至 $ 3 $ 月 $ 13 $ 日中的某一天到达该市，并停留 $ 2 $ 天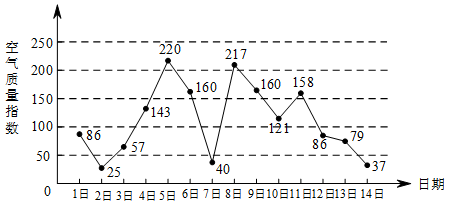．  2022-04-17 19:40:22
16402 599165be2bfec200011df77b 高中 解答题 高考真题 某单位招聘面试，每次从试题库中随机调用一道试题．若调用的是 $ A $ 类型试题，则使用后该试题回库，并增补一道 $ A $ 类型试题和一道 $ B $ 类型试题入库，此次调题工作结束；若调用的是 $ B $ 类型试题，则使用后该试题回库，此次调题工作结束．试题库中现共有 $ n+m $ 道试题，其中有 $ n $ 道 $ A $ 类型试题和 $ m $ 道 $ B $ 类型试题．以 $ X $ 表示两次调题工作完成后，试题库中 $ A $ 类试题的数量． 2022-04-17 19:37:22
16396 599165be2bfec200011df734 高中 解答题 高考真题 电视传媒公司为了解某地区电视观众对某类体育节目的收视情况，随机抽取了 $ 100 $ 名观众进行调查．下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图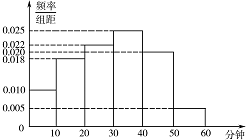： 将日均收看该体育节目时间不低于 $ 40 $ 分钟的观众称为"体育迷"．
附：$ \chi^ 2={\dfrac{n\left(n_{11}n_{22}-n_{12}n_{21}\right)^2}{n_{1+}n_{2+}n_{+1}n_{+2}}}$，\[ \begin{array}{c|cc}
P\left(\chi ^2\geqslant k\right)& 0.05 &0.01 \\ \hline
k& 3.841& 6.635 \end{array} \]		 2022-04-17 19:34:22
16389 599165bd2bfec200011df5a6 高中 解答题 高考真题 某班 $ 50 $ 位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：$\left[ {40,50} \right)$，$\left[ {50,60} \right)$，$\left[ {60,70} \right)$，$\left[ {70,80} \right)$，$\left[ {80,90} \right)$，$\left[ {90,100} \right]$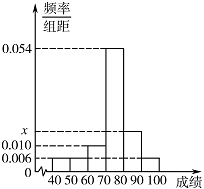．  2022-04-17 19:31:22
16049 601b636725bdad0009f73f9f 高中 解答题 自招竞赛 设复数集$$V=\{\sqrt{2}i,-\sqrt{2}i, \frac{1}{\sqrt{8}}(1+i), \frac{1}{\sqrt{8}}(-1+i),\frac{1}{\sqrt{8}}(1-i),\frac{1}{\sqrt{8}}(-1-i)\}.$$对任意 $1\leqslant j\leqslant 12$，复数 $z_j$ 的值从 $V$ 中等可能地随机选取，且所有 $z_j$ 的取值都是互相独立的．记 $\displaystyle P=\prod^{12}_{j=1}z_j$，试求 $P=-1$ 的概率． 2022-04-17 19:16:19
16042 60092f8c8874860009b91fc9 高中 解答题 自招竞赛 给定正整数 $n$．抛掷一枚均匀的硬币 $n$ 次，并将结果记录为一个由 $0$ 和 $1$ 组成的数列（即若第 $i$ 次抛掷结果是正面向上，则令数列第 $i$ 项等于 $1$，否则令其等于 $0$）．如果该数列中连续若干项（允许只有一项）都是同一个数，则称这些项为一段，其项数就是该段的长度．如果某一段后没有紧跟一段长度更长的段，则称其为好段．设好段的数目为随机变量 $X_n$，试求 $X_n$ 的数学期望（均值）．例如，数列 $1,0,0,1,1,0,1,1,1,0$ 共有 $6$ 段，每一段的长度分别为 $1,2,2,1,3,1$，其中第 $2,3,5,6$ 段后没有紧跟长度更长的段，故在该数列中，有 $X_{10}=4$． 2022-04-17 19:12:19
16007 602e09e925bdad000ac4d55a 高中 解答题 自招竞赛 在一个游戏中，甲，乙两人轮流抛掷一枚均匀的硬币．数列 $\{a_n\}$ 满足：$a_1=4,a_2=3, a_n=a_{n-1}+a_{n-2}$（$n\geqslant 3$）．在第 $n$ 次抛掷中，若硬币正面向上，则甲付给乙 $a_n$ 个游戏币；若反面向上，则乙付给甲 $a_n$ 个游戏币．试求在 $3000$ 次抛掷后，甲的游戏币数量比开始时多的概率． 2022-04-17 19:53:18
15751 590824f3060a050008e621fb 高中 解答题 高中习题 已知 $(1-x)^n=a_0+a_1x+a_2x^2+\cdots +a_nx^n$，求 $\displaystyle \sum\limits_{k=0}^n\dfrac{1}{a_k}$． 2022-04-17 19:36:16
15739 5909773f39f91d0009d4bfd5 高中 解答题 高中习题 求证：$\dfrac{1}{\sin^2\dfrac{\pi}{2n+1}}+\dfrac{1}{\sin^2\dfrac{2\pi}{2n+1}}+\cdots +\dfrac{1}{\sin^2\dfrac{2n\pi}{2n+1}}=\dfrac 43n(n+1)$． 2022-04-17 19:30:16
15731 590987b439f91d0008f05067 高中 解答题 自招竞赛 $a,b,c$ 是三个不同的正整数，$abc=11\cdot 21 \cdot 31 \cdot 41\cdot 51\cdot 61$．求所有满足要求的集合 $\{ a,b,c \}$ 的个数． 2022-04-17 19:26:16
15730 590988bf39f91d000a7e457a 高中 解答题 自招竞赛 用 $4$ 种不同的颜色给下图中的 $6$ 个扇环染色，每个扇环只染一种颜色，相邻的扇环染不同的颜色，求所有染色的方法数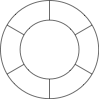． 2022-04-17 19:25:16
15729 59098a5139f91d0007cc93bd 高中 解答题 自招竞赛 Beatrix在一个 $6\times6$ 的棋盘上放了 $6$ 枚棋子，任意两枚棋子既不在同一行也不在同一列．定义某一枚棋子的分值为其所在位置的行数与列数之和，定义 $6$ 枚棋子的总分值为这 $6$ 枚棋子分值的最小值．将所有排列中 $6$ 枚棋子的总分值的平均数记为 $\dfrac{p}{q}$，其中 $p,q$ 为互质的正整数．求 $p+q$ 的值． 2022-04-17 19:24:16
0.185551s