某班 $ 50 $ 位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:$\left[ {40,50} \right)$,$\left[ {50,60} \right)$,$\left[ {60,70} \right)$,$\left[ {70,80} \right)$,$\left[ {80,90} \right)$,$\left[ {90,100} \right]$.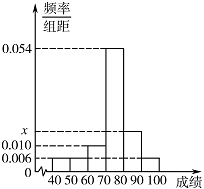

【难度】
【出处】
2012年高考广东卷(理)
【标注】
-
求图中 $x$ 的值;标注答案略解析由频率分布直方图知\[\left(0.006 \times 3 + 0.01 + x + 0.054 \right) \times 10 = 1 , \]解得\[x = 0.018.\]
-
从成绩不低于 $ 80 $ 分的学生中随机选取 $ 2 $ 人,该 $ 2 $ 人中成绩在 $ 90 $ 分以上(含 $ 90 $ 分)的人数记为 $\xi $,求 $\xi $ 的数学期望.标注答案略解析由频率分布直方图知成绩不低于 $ 80 $ 分的学生人数为\[\left(0.018 + 0.006 \right) \times 10 \times 50 = 12,\]成绩在 $ 90 $ 分以上(含 $ 90 $ 分)的人数为\[0.006 \times 10 \times 50 = 3. \]因此 $\xi $ 可能取 $0,1,2 $ 三个值.\[\begin{split} P\left( \xi =0\right) & = \dfrac{{\mathrm{C}}_9^2}{{\mathrm{C}}_{12}^2} = \dfrac 6 {11} , \\ P\left( \xi = 1\right) & = \dfrac{{{\mathrm{C}}_9^1} \cdot {{\mathrm{C}}_3^1}}{{\mathrm{C}}_{12}^2} = \dfrac 9 {22} , \\ P\left( \xi =2\right) & = \dfrac{{\mathrm{C}}_3^2}{{\mathrm{C}}_{12}^2} = \dfrac 1 {22} .\end{split}\]$\xi $ 的分布列为\[\begin{array}{|c|c|c|c|} \hline
\xi & 0 & 1 & 2 \\ \hline
P & \frac{6}{11} & \frac{9}{22} & \frac{1}{22} \\ \hline \end{array}\]故\[ E\left(\xi\right) = 0 \times \dfrac 6 {11} + 1 \times \dfrac 9 {22} + 2 \times \dfrac 1 {22} = \dfrac 1 2 .\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2