用 $4$ 种不同的颜色给下图中的 $6$ 个扇环染色,每个扇环只染一种颜色,相邻的扇环染不同的颜色,求所有染色的方法数.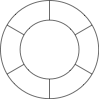

【难度】
【出处】
2016年第34届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
$732$
【解析】
一般的,我们来考虑用 $k$ 种不同的颜色给 $n$ 个扇环染色的方法数 $a_n$.
解法一 先考虑排列,然后再考虑圆排列,有$$a_n+a_{n-1}=k\cdot (k-1)^{n-1},\quad a_1=0,\quad a_2=k(k-1),$$解得$$a_n=(k-1)^n+(k-1)\cdot (-1)^n.$$解法二 从已有的圆排列得到更长的圆排列,有$$a_n=(k-2)a_{n-1}+(k-1)a_{n-2},\quad a_1=0,\quad a_2=k(k-1),$$解得$$a_n=(k-1)^n+(k-1)\cdot (-1)^n.$$
答案
解析
备注