经销商经销某种农产品,在一个销售季度内,每售出 $1 {\mathrm{t}}$ 该产品获利润 $500$ 元,未售出的产品,每 $1 {\mathrm{t}}$ 亏损 $300$ 元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了 $130 {\mathrm {t}}$ 该农产品.以 $X$(单位:$ {\mathrm {t}}$,$100 \leqslant X \leqslant 150$)表示下一个销售季度内的市场需求量,$T$(单位:元)表示下一个销售季度内经销该农产品的利润.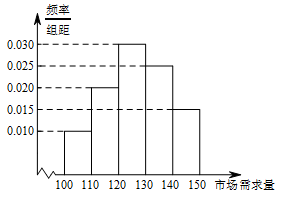

【难度】
【出处】
2013年高考新课标Ⅱ卷(理)
【标注】
-
将 $T$ 表示为 $X$ 的函数;标注答案$T = {\begin{cases}
800X - 39000,&100 \leqslant X < 130, \\
65000,&130 \leqslant X \leqslant 150 \\
\end{cases}}$解析本题考查实际应用问题,根据题意表达此分段函数即可.这是一个分段函数.
当 $X \in \left[ {100,130} \right)$ 时,\[\begin{split}T &= 500X - 300\left( {130 - X} \right) \\&= 800X - 39000;\end{split}\]当 $X \in \left[ {130,150} \right]$ 时,\[\begin{split}T &= 500 \times 130 \\&= 65000.\end{split}\]所以\[T = {\begin{cases}800X - 39000,&100 \leqslant X < 130, \\
65000,&130 \leqslant X \leqslant 150 .\\
\end{cases}}\] -
根据直方图估计利润 $T$ 不少于 $57000$ 元的概率;标注答案$0.7$解析本题考查频率分布直方图的相关知识.由第一小问,得到满足题意的 $X$ 的取值范围,再结合频率分布直方图,问题得到解决.由(1)知利润 $T$ 不少于 $ 57000 $ 元,当且仅当 $120 \leqslant X \leqslant 150$.
由直方图知需求量 $X \in \left[ {120,150} \right]$ 的频率为 $0.7$,所以下一个销售季度内的利润 $T$ 不少于 $ 57000 $ 元的概率的估计值为 $0.7$. -
在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量 $X \in \left[ {100,110} \right)$,则取 $X = 105$,且 $X = 105$ 的概率等于需求量落入 $\left[ {100,110} \right)$ 的频率),求 $T$ 的数学期望.标注答案$59400$解析本题考查离散型随机变量及其分布列.依题意可得 $T$ 的分布列为\[\begin{array}{|c|c|c|c|c|} \hline T & 45000 & 53000 & 61000 & 65000 \\ \hline P & 0.1 & 0.2 & 0.3 & 0.4 \\ \hline\end{array}\]所以\[\begin{split}E\left(T\right) &\overset{\left[a\right]}= 45000 \times 0.1 + 53000 \times 0.2 + 61000 \times 0.3 + 65000 \times 0.4 \\&= 59400.\end{split}\](推导中用到[a])
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3