重置
序号 ID 年级 类型 来源 摘要 创建时间
22202 5a0956a98621cc0009c5fdfe 高中 解答题 自招竞赛 某电视厂家准备在元旦期间举办促销活动，现根据近七年的广告费与销售量的数据确定此次广告费支出．广告费支出 $x_i$（万元）和销售量 $y_i$（万台）的数据如下：\[\begin{array}{|c|c|c|c|c|c|c|c|}\hline \text{年份}&2011&2012&2013&2014&2015&2016&2017 \\ \hline \text{广告费支出}&1&2&4&6&11&13&19\\ \hline \text{销售量}&1.9&3.2&4.0&4.4&5.2&5.3&5.4 \\ \hline \end{array}\]参考公式：$$\hat b=\dfrac{\sum\limits_{i=1}^{n}{x_i y_i}-n\overline x\overline y}{\sum\limits_{i=1}^{n}{x_i^2}-n{\overline x}^2}=\dfrac{\sum\limits_{i=1}^{n}\left(x_i-\overline x\right)\left(y_i-\overline y\right)}{\sum\limits_{i=1}^{n}\left(x_i-\overline x\right)^2} , \hat a=\overline y-\hat b\overline x.$$参考数据：$\sqrt 5=2.24 $． 2022-04-17 20:00:16
21977 5a40a828fab70800079179b5 高中 解答题 自招竞赛 身体质量指数BMI（简称体质指数）是目前国际上蝉蛹的衡量人体胖瘦程度以及是否健康的一个标准．现为分析胖瘦程度对空腹血糖的影响，从志愿者中随机抽取 $12$ 名志愿者测定BMI值及空腹血糖GLU指标（单位：${\rm mol}/{\rm L}$）如下表所示（$i$ 表示人员编号，$x_i,y_i$ 分别表示编号为 $i$ 的人员的BMI值和GLU指标值）：\[\begin{array}{c|cccccccccccc}\hline
i&1&2&3&4&5&6&7&8&9&10&11&12\\ \hline
x_i&14&17&18&19&20&22&23&26&27&29&30&31\\ \hline
y_i&2.5&4.5&4.8&4.9&5.5&5.6&5.8&6.1&6.4&6.9&7.1&9.5\\ \hline
\end{array}\]		 2022-04-17 20:57:13
20980 5c6e4c3b210b2877bbec8d55 高中 解答题 自招竞赛 从1到1000的整数中，有多少个能够表示为两个非负整数的平方差？ 2022-04-17 20:42:04
20834 5c74abaa210b284290fc22ba 高中 解答题 自招竞赛 设 $a b c$ 是三个正整数，满足 $a=b+60$，$\sqrt{a}+\sqrt{b}=\sqrt{c}$，且 $\sqrt{c}$ 不是整数（即 $c$ 不是一个完全平方数）．令 $s=a+b$，求 $s$ 的最大可能值． 2022-04-17 20:27:03
19318 5c6b70b0210b281db9f4c85e 高中 解答题 自招竞赛 一生物学家想要计算一个湖中鱼的条数，在5月1日，她随机地捕捉60条鱼，并对它们作了标记后放回湖中．在9月1日，她再随机地捕捉70条鱼，发现其中3条鱼是有标记的．为了计算5月1日这湖中鱼的条数，她假定5月1日湖中鱼的 $25\%$ 到9月1日已不在湖中（由于死亡和迁出），9月1日湖中鱼的 $40\%$ 5月1日并不在湖中（由于出生和迁入），而且9月1日抽样所得的无标记及有标记的鱼数是有代表性的，这位生物学家算出的5月1日湖中鱼数是多少？ 2022-04-17 19:34:49
17185 5e65bb3c210b280d3782255e 高中 解答题 高考真题 为了了解甲，乙两种离子在小鼠体内的残留程度，进行如下实验．将 $200$ 只小鼠随机分成 $A,B$ 两组，每组 $100$ 只，其中 $A$ 组小鼠给服甲离子溶液，$B$ 组小鼠给服乙离子溶液，每只小鼠给服的溶液体积相同，摩尔浓度相同．经过一段时间启用某种科学方法测算出残留在小鼠体内离子的百分比，根据实验数据分别得到如下直方图：
记 $C$ 为事件："乙离子残留在体内的百分比不低于 $5.5$ "，根据直方图得到的 $P(C)$ 的估计值为 $0.70$．
（1）求乙离子残留百分比直方图中 $a,b$ 的值；
（2）分别估计甲，乙离子残留百分比的平均值（同一组中的数据用该组区间的中点值为代表）．		 2022-04-17 19:59:29
17176 5e61b332210b280d36111796 高中 解答题 高考真题 某行业主管部门为了解本行业中小企业的情况，随机调查了 $100$ 个企业，得到这些企业第一季度相对于前一年第一季度产值增长率 $y$ 的频数分布表．\[\begin{array}{|c|c|c|c|c|c|}\hline y\text{的分组}&[-0.20,0)&[0,0.20)&[0.20,0.40)&[0.40,0.60)&[0.60,0.80)\\\hline \text{企业数}&2&24&53&14&7\\\hline\end{array}\]（1）分别估计这类企业中产值增长率不低于 $40\%$ 的企业比例，产值负增长二的企业比例；
（2）求这类企业产值增长率的平均数与标准差的估值（同一组中的数据用该组区间的中点值为代表）．（精确到 $0.01$）		 2022-04-17 19:54:29
17171 5e5f1b26210b280d361116ee 高中 解答题 高考真题 某商场为提高服务质量，随机调查了 $50$ 名男顾客和 $50$ 名女顾客，每位顾客对该商场的服务给出满意或不满意的评价，得到下面的联表：\[\begin{array}{|c|c|c|}\hline &\text{满意}&\text{不满意}\\\hline \text{男顾客}&40&10\\\hline \text{女顾客}&30&20\\\hline\end{array}\]（1）分别估计男，女顾客对该商场服务满意的概率；
（2）能否有 $95\%$ 的把握认为男，女顾客对该商场服务的评价有差异？		 2022-04-17 19:50:29
17164 5e5c70aa210b280d378223f8 高中 解答题 高考真题 $2019$ 年，我国施行个人所得税专项附加扣除办法，涉及子女教育，继续教育，大病医疗，住房贷款利息或者住房佣金，赡养老人等六项专项附加扣除．某单位老，中，青员工分别有 $72,108,120$ 人，现采用分层抽样的方法，从该单位上述员工中抽取 $25$ 人调查专项附加扣除的享受情况．
（I）应从老，中，青员工中分别抽取多少人？
（II）抽取的 $25$ 人中，享受至少两项专项附加扣除的员工有 $6$ 人，分别记为 $A,B,C,D,E,F$，享受情况如右表，其中“$\bigcirc$”表示享受，“$\times$”表示不享受．现从这 $6$ 个人中随机抽取 $2$ 人接受采访．\[\begin{array}{|c|c|c|c|c|c|c|}\hline \text{项目\员工}&A&B&C&D&E&F\\\hline \text{子女教育}&\bigcirc&\bigcirc&\times&\bigcirc&\times&\bigcirc\\\hline \text{继续教育}&\times&\times&\bigcirc&\times&\bigcirc&\bigcirc\\\hline \text{大病医疗}&\times&\times&\times&\bigcirc&\times&\times\\\hline
\text{住房贷款利息}&\bigcirc&\bigcirc&\times&\times&\bigcirc&\bigcirc\\\hline \text{住房租金}&\times&\times&\bigcirc&\times&\times&\times\\\hline \text{赡养老人}&\bigcirc&\bigcirc&\times&\times&\times&\bigcirc\\\hline\end{array}\]（i）试用所给字母列举出所有可能的抽取结果；
（ii）设 $M$ 为事件“抽取的 $2$ 人享受的专项附加扣除至少有一项相同”，求事件 $M$ 发生的概率．		 2022-04-17 19:48:29
17144 5e4f4e5c210b280d36111426 高中 解答题 高考真题 改革开放以来，人们的支付方式发生了巨大改变．近年来，移动支付已成为主要支付方式之一．为了解某校学生上个月 $A,B$ 两种移动支付方式的使用情况，从全校所有的 $1000$ 学生中随机抽取了 $100$ 人，发现样本中 $A,B$ 两种支付方式都不使用的有 $5$ 人，样本中仅使用 $A$ 和仅使用 $B$ 的学生的支付金额分布情况如下：\[\begin{array}{|c|c|c|}\hline\text{支付方式\支付金额(元)}&\text{不大于}2000\text{元}&\text{大于}2000\text{元}\\\hline\text{仅使用}A&27\text{人}&3\text{人}\\\hline\text{仅使用}B&24\text{人}&1\text{人}\\\hline\end{array}\]（I）估计该学生上个月 $A,B$ 两种支付方式都使用的人数；
（II）从样本仅使用 $B$ 的学生中随机抽取 $1$ 人，求该学生上个月支付金额大于 $2000$ 元的概率；
（III）已知上个月样本学生的支付方式在本月没有变化．现从样本仅使用 $B$ 的学生中，随机抽查 $1$ 人，发现他本月的支付金额都大于 $2000$ 元．结合（II）的结果，能否认为样本仅使用 $B$ 的学生中本月支付金额大于 $2000$ 元的人数有变化？说明理由．		 2022-04-17 19:37:29
17138 5e4ca50f210b280d3782218e 高中 解答题 高考真题 改革开放以来，人们的支付方式发生了巨大改变．近年来，移动支付已成为主要支付方式之一．为了解某校学生上个月 $A,B$ 两种移动支付方式的使用情况，从全校学生中随机抽取了 $100$ 人，发现样本中 $A,B$ 两种支付方式都不使用的有 $5$ 人，样本中仅使用 $A$ 和仅使用 $B$ 的学生的支付金额分布情况如下：\[\begin{array}{|c|c|c|c|}\hline\text{支付方式\支付金额(元)}&(0,1000]&(1000,2000]&\text{大于}2000\\\hline\text{仅使用}A&18\text{人}&9\text{人}&3\text{人}\\\hline\text{仅使用}B&10\text{人}&14\text{人}&1\text{人}\\\hline\end{array}\]（I）从全校学生中随机抽取 $1$ 人，估计该学生上个月 $A,B$ 两种支付方式都使用的频率；
（II）从样本仅使用 $A$ 和仅使用 $B$ 的学生中各随机抽取 $1$ 人，以 $X$ 表示这 $2$ 人中上个月支付金额大于 $1000$ 元的人数，求 $X$ 的分布列和数学期望；
（III）已知上个月样本学生的支付方式在本月没有变化．现从样本仅使用 $A$ 的学生中，随机抽查 $3$ 人，发现他们本月的支付金额都大于 $2000$ 元．根据抽查结果，能否认为样本仅使用 $A$ 的学生中本月支付金额大于 $2000$ 元的人数有变化？说明理由．		 2022-04-17 19:34:29
17107 5e3ccda6210b286bd531929a 高中 解答题 高考真题 为了了解甲，乙两种离子在小鼠体内的残留程度，进行如下实验．将 $200$ 只小鼠随机分成 $A,B$ 两组，每组 $100$ 只，其中 $A$ 组小鼠给服甲离子溶液，$B$ 组小鼠给服乙离子溶液，每只小鼠给服的溶液体积相同，摩尔浓度相同．经过一段时间启用某种科学方法测算出残留在小鼠体内离子的百分比，根据实验数据分别得到如下直方图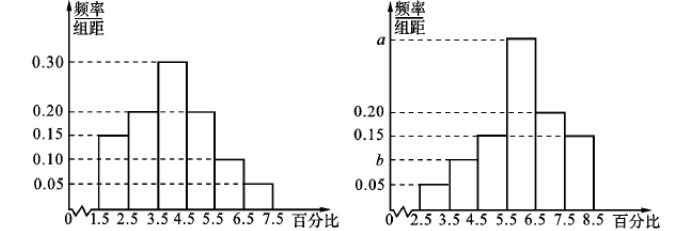：记 $C$ 为事件："乙离子残留在体内的百分比不低于 $5.5$ "，根据直方图得到的 $P(C)$ 的估计值为 $0.70$．
（1）求乙离子残留百分比直方图中 $a,b$ 的值；
（2）分别估计甲，乙离子残留百分比的平均值（同一组中的数据用该组区间的中点值为代表）．		 2022-04-17 19:17:29
17016 599165ca2bfec200011e1c9d 高中 解答题 高考真题 海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了 $100$ 个网箱，测量各箱水产品的产量（单位：$\rm {kg}$），其频率分布直方图如下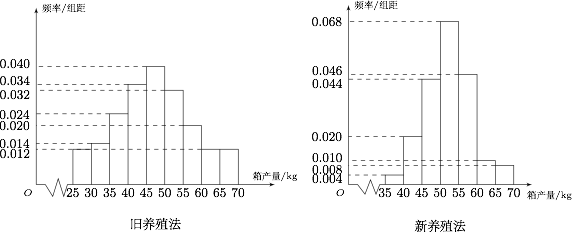：  2022-04-17 19:27:28
16929 599165c82bfec200011e1734 高中 解答题 高考真题 我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准 $x$（吨），一位居民的月用水量不超过 $x$ 的部分按平价收费，超出 $x$ 的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年 $100$ 位居民每人的月均用水量（单位：吨），将数据按照 $\left[0,0.5\right),\left[0.5,1\right),\cdots,\left[4,4.5\right)$ 分成 $9$ 组，制成了如图所示的频率分布直方图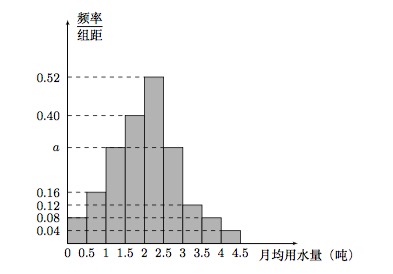．  2022-04-17 19:35:27
16924 599165c82bfec200011e16b7 高中 解答题 高考真题 $A$、$B$、$C$ 三个班共有 $100$ 名学生，为调查他们的体育锻炼情况，通过分层抽样获得了部分学生一周的锻炼时间，数据如下表（单位：小时）：\[\begin{array}{|c|cccccccc|} \hline
A班 & 6& 6.5&7&7.5&8 \\\hline
B班&6&7&8&9&10&11&12 \\\hline
C班&3&4.5&6&7.5&9&10.5&12&13.5\\\hline
\end{array}\]		 2022-04-17 19:32:27
16912 599165c82bfec200011e150f 高中 解答题 高考真题 下图是我国 $2008$ 年至 $2014$ 年生活垃圾无害化处理量（单位：亿吨）的折线图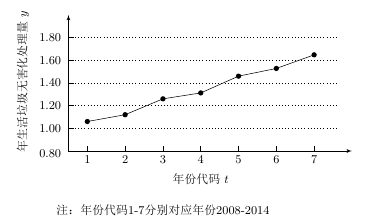． 附注：
参考数据：$\displaystyle \sum\limits_{i=1}^7{y_i}=9.32$，$\displaystyle \sum\limits_{i=1}^{7}t_iy_i=40.17$，$\displaystyle \sqrt{\sum\limits_{i=1}^7\left(y_i-\bar y\right)^2}=0.55$，$\sqrt 7\approx 2.646$．
参考公式：相关系数 $\displaystyle r=\dfrac{\sum\limits_{i=1}^n\left(t_i-\bar t\right)\left(y_i-\bar y\right)}{\sqrt{\sum\limits_{i=1}^n\left(t_i-\bar t\right)^2\sum\limits_{i=1}^n\left(y_i-\bar y\right)^2}}$
回归方程 $\hat y=\hat a+\hat b t$ 中斜率和截距的最小二乘估计公式分别为：
$\displaystyle \hat b=\dfrac {\sum\limits_{i=1}^n \left(t_i-\bar t\right)\left(y_i-\bar y\right)}{\sum\limits_{i=1}^{n}\left(t_i-\bar t\right)^2}$，$\hat a=\bar y -\hat b \bar t$．		 2022-04-17 19:26:27
16845 599165c42bfec200011e0a95 高中 解答题 高考真题 某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费 $ x $（单位：千元）对年销售量 $ y $（单位：$ t $）和年利润 $ z $（单位：千元）的影响．对近 $ 8 $ 年的年宣传费 $ x_i $ 和年销售量 $ y_i\left(i=1,2,\cdots,8\right) $ 数据作了初步处理，得到下面的散点图及一些统计量的值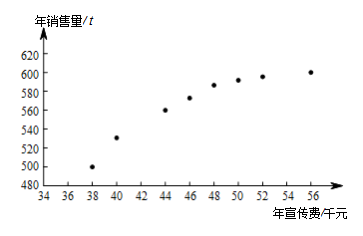． \[ \begin{array}{|c|c|c|c|c|c|c|}\hline
\overline x& \overline y& \overline w &\sum\limits_{i=1}^8\left(x_i-\overline x\right)^2& \sum\limits_{i=1}^8\left(w_i-\overline w\right)^2& \sum\limits_{i=1}^8\left(x_i-\overline x\right)\left(y_i-\overline y\right)& \sum\limits_{i=1}^8\left(w_i-\overline w\right)\left(y_i-\overline y\right)\\ \hline
46.6& 563& 6.8& 289.8& 1.6& 1469 &108.8\\ \hline
\end{array} \]表中 $ w_i=\sqrt{x_i} $，$\displaystyle \overline w=\dfrac 18\sum\limits_{i=1}^8w_i $．
附：对于一组数据 $\left(u_1,v_1\right)$，$\left(u_2,v_2\right)$，$\cdots$，$\left(u_n,v_n\right)$，其回归直线 $v=\alpha+\beta u$ 的斜率和截距的最小二乘估计分别为 $\displaystyle \hat \beta=\dfrac{\sum\limits_{i=1}^n\left(u_i-\bar u\right)\left(v_i-\bar v\right)}{\sum\limits_{i=1}^n\left(u_i-\bar u\right)^2}$，$\hat \alpha=\bar v-\hat \beta\bar u$．		 2022-04-17 19:48:26
16841 599165c42bfec200011e0a02 高中 解答题 高考真题 某公司为了解用户对其产品的满意度，从 $ A $，$ B $ 两地区分别随机调查了 $20$ 个用户，得到用户对产品的满意度评分如下：\[ \begin{array}{ccccccccccc}
A地区 :&62&73&81&92&95&85&74&64&53&76\\
&78&86&95&66&97&78&88&82&76&89\\
B地区 :&73&83&62&51&91&46&53&73&64&82\\
&93&48&65&81&74&56&54&76&65&79\\
\end{array} \]		 2022-04-17 19:45:26
16831 599165c42bfec200011e0946 高中 解答题 高考真题 $A$，$B$ 两组各有 $7$ 位病人，他们服用某种药物后的康复时间（单位：天）记录如下：\[\begin{array}{cccccccc}
A 组:&10,&11,&12,&13,&14,&15,&16;\\
B 组:&12,&13,&15,&16,&17,&14,&a.\\
\end{array}\]假设所有病人的康复时间相互独立，从 $A$，$B$ 两组随机各选 $1$ 人，$A$ 组选出的人记为甲，$B$ 组选出的人记为乙．		 2022-04-17 19:39:26
16711 5f0142d7210b28774f712f03 高中 解答题 高中习题 化简： 2022-04-17 19:29:25
0.187401s