某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费 $ x $（单位：千元）对年销售量 $ y $（单位：$ t $）和年利润 $ z $（单位：千元）的影响．对近 $ 8 $ 年的年宣传费 $ x_i $ 和年销售量 $ y_i\left(i=1,2,\cdots,8\right) $ 数据作了初步处理，得到下面的散点图及一些统计量的值．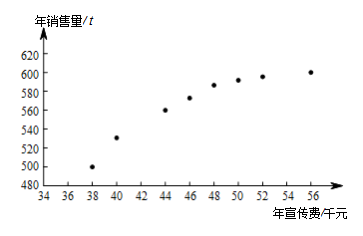
\[ \begin{array}{|c|c|c|c|c|c|c|}\hline
\overline x& \overline y& \overline w &\sum\limits_{i=1}^8\left(x_i-\overline x\right)^2& \sum\limits_{i=1}^8\left(w_i-\overline w\right)^2& \sum\limits_{i=1}^8\left(x_i-\overline x\right)\left(y_i-\overline y\right)& \sum\limits_{i=1}^8\left(w_i-\overline w\right)\left(y_i-\overline y\right)\\ \hline
46.6& 563& 6.8& 289.8& 1.6& 1469 &108.8\\ \hline
\end{array} \]表中 $ w_i=\sqrt{x_i} $，$\displaystyle \overline w=\dfrac 18\sum\limits_{i=1}^8w_i $．
附：对于一组数据 $\left(u_1,v_1\right)$，$\left(u_2,v_2\right)$，$\cdots$，$\left(u_n,v_n\right)$，其回归直线 $v=\alpha+\beta u$ 的斜率和截距的最小二乘估计分别为 $\displaystyle \hat \beta=\dfrac{\sum\limits_{i=1}^n\left(u_i-\bar u\right)\left(v_i-\bar v\right)}{\sum\limits_{i=1}^n\left(u_i-\bar u\right)^2}$，$\hat \alpha=\bar v-\hat \beta\bar u$．
\[ \begin{array}{|c|c|c|c|c|c|c|}\hline\overline x& \overline y& \overline w &\sum\limits_{i=1}^8\left(x_i-\overline x\right)^2& \sum\limits_{i=1}^8\left(w_i-\overline w\right)^2& \sum\limits_{i=1}^8\left(x_i-\overline x\right)\left(y_i-\overline y\right)& \sum\limits_{i=1}^8\left(w_i-\overline w\right)\left(y_i-\overline y\right)\\ \hline
46.6& 563& 6.8& 289.8& 1.6& 1469 &108.8\\ \hline
\end{array} \]表中 $ w_i=\sqrt{x_i} $，$\displaystyle \overline w=\dfrac 18\sum\limits_{i=1}^8w_i $．
附：对于一组数据 $\left(u_1,v_1\right)$，$\left(u_2,v_2\right)$，$\cdots$，$\left(u_n,v_n\right)$，其回归直线 $v=\alpha+\beta u$ 的斜率和截距的最小二乘估计分别为 $\displaystyle \hat \beta=\dfrac{\sum\limits_{i=1}^n\left(u_i-\bar u\right)\left(v_i-\bar v\right)}{\sum\limits_{i=1}^n\left(u_i-\bar u\right)^2}$，$\hat \alpha=\bar v-\hat \beta\bar u$．
【难度】
【出处】
2015年高考全国Ⅰ卷（文）
【标注】
-
根据散点图判断，$y=a+bx$ 与 $y=c+d\sqrt x $ 哪一个适宜作为年销售量 $y$ 关于年宣传费 $x$ 的回归方程类型？（给出判断即可，不必说明理由）标注答案$y=c+d\sqrt x$ 适宜作为 $y$ 关于 $x$ 的回归方程类型解析注意图中散点没有集中在某条直线附近，应进行适当变形．由散点图可知，年销售量 $y$ 与年宣传费 $x$ 非线性相关，故 $y=c+d\sqrt x$ 适宜作为 $y$ 关于 $x$ 的回归方程类型．
-
根据 $(1)$ 的判断结果及表中数据，建立 $y$ 关于 $x$ 的回归方程；标注答案$\hat y=100.6+68\sqrt x$解析根据题目所给数据与公式进行计算，得到回归方程．令 $\omega =\sqrt x$，先建立 $y$ 关于 $\omega$ 的线性回归方程．
因为\[\begin{split}\hat d&\overset{\left[a\right]}=\dfrac {\sum\limits_{i=1}^{8}\left(w_i-\bar w\right)\left(y_i-\bar y\right)}{\sum\limits_{i=1}^{8}{\left(w_i-\bar w\right)}^2}\\&=\dfrac {108.8}{1.6}\\&=68,\end{split}\]所以\[\begin{split}\hat c&\overset{\left[a\right]}=\bar y-\hat d\bar w\\&=563-68\times 6.8\\&=100.6,\end{split}\]（推导中用到：$\left[a\right]$）
所以 $y$ 关于 $\omega$ 的线性回归方程为\[\hat y=100.6+68\omega,\]所以 $y$ 关于 $x$ 的回归方程为\[\hat y=100.6+68\sqrt x.\] -
已知这种产品的年利润 $z$ 与 $x$，$y$ 的关系为 $z=0.2y-x$．根据 $(2)$ 的结果回答下列问题：
（i）年宣传费 $x=49$ 时，年销售量及年利润的预报值是多少？
（ii）年宣传费 $x$ 为何值时，年利润的预报值最大？标注答案当宣传费为 $49$ 千元时，年销售量及年利润预报值分别为 $576.6$ 千元和 $66.32$ 千元；当 $x=46.24$ 时，年利润的预报值最大解析利用前面的回归方程，进行数据预测．（i）因为 $y$ 关于 $x$ 的回归方程为 $\hat y=100.6+68\sqrt x$，所以当 $x=49$ 时，年销售量 $y$ 的预报值\[\hat y\overset{\left[a\right]}=100.6+68\times \sqrt {49}=576.6.\]（推导中用到：$\left[a\right]$）
所以年利润 $z$ 的预报值\[\begin{split}\hat z&=0.2\hat y-x\\&=0.2\times 576.6-49\\&=66.32.\end{split}\]所以当宣传费为 $49$ 千元时，年销售量及年利润预报值分别为 $576.6$ 千元和 $66.32$ 千元．
（ii）因为年利润 $z$ 的预报值\[ \begin{split}
\hat{z}&=0.2\hat y-x \\
&=0.2\left(100.6+68\sqrt x\right)-x \\
&=-x+13.6\sqrt x+20.12.
\end{split} \]所以当 $\sqrt x=6.8$，即 $x=46.24$ 时，年利润的预报值最大．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
