下图是我国 $2008$ 年至 $2014$ 年生活垃圾无害化处理量(单位:亿吨)的折线图.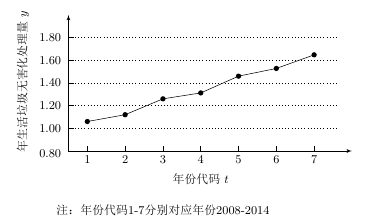 附注:
附注:
参考数据:$\displaystyle \sum\limits_{i=1}^7{y_i}=9.32$,$\displaystyle \sum\limits_{i=1}^{7}t_iy_i=40.17$,$\displaystyle \sqrt{\sum\limits_{i=1}^7\left(y_i-\bar y\right)^2}=0.55$,$\sqrt 7\approx 2.646$.
参考公式:相关系数 $\displaystyle r=\dfrac{\sum\limits_{i=1}^n\left(t_i-\bar t\right)\left(y_i-\bar y\right)}{\sqrt{\sum\limits_{i=1}^n\left(t_i-\bar t\right)^2\sum\limits_{i=1}^n\left(y_i-\bar y\right)^2}}$
回归方程 $\hat y=\hat a+\hat b t$ 中斜率和截距的最小二乘估计公式分别为:
$\displaystyle \hat b=\dfrac {\sum\limits_{i=1}^n \left(t_i-\bar t\right)\left(y_i-\bar y\right)}{\sum\limits_{i=1}^{n}\left(t_i-\bar t\right)^2}$,$\hat a=\bar y -\hat b \bar t$.
 附注:
附注:参考数据:$\displaystyle \sum\limits_{i=1}^7{y_i}=9.32$,$\displaystyle \sum\limits_{i=1}^{7}t_iy_i=40.17$,$\displaystyle \sqrt{\sum\limits_{i=1}^7\left(y_i-\bar y\right)^2}=0.55$,$\sqrt 7\approx 2.646$.
参考公式:相关系数 $\displaystyle r=\dfrac{\sum\limits_{i=1}^n\left(t_i-\bar t\right)\left(y_i-\bar y\right)}{\sqrt{\sum\limits_{i=1}^n\left(t_i-\bar t\right)^2\sum\limits_{i=1}^n\left(y_i-\bar y\right)^2}}$
回归方程 $\hat y=\hat a+\hat b t$ 中斜率和截距的最小二乘估计公式分别为:
$\displaystyle \hat b=\dfrac {\sum\limits_{i=1}^n \left(t_i-\bar t\right)\left(y_i-\bar y\right)}{\sum\limits_{i=1}^{n}\left(t_i-\bar t\right)^2}$,$\hat a=\bar y -\hat b \bar t$.
【难度】
【出处】
2016年高考全国丙卷(文)
【标注】
-
由折线图看出,可用线性回归模型拟合 $y$ 与 $t$ 的关系,请用相关系数加以说明;标注答案略解析相关系数可以用来刻画两个变量的线性相关性的强弱,$|r|$ 越接近于 $1$,表明两个变量的线性相关性越强.根据已知可求得\[\bar t=4,\sum \limits_{i=1}^7\left(t_i-\bar t\right)^2=28,\sqrt{\sum\limits _{i=1}^7\left(y_i-\bar y\right)^2}=0.55,\]\[\sum \limits_{i=1}^7\left(t_i-\bar t\right)\left(y_i-\bar y\right)=\sum \limits_{i=1}^7t_iy_i-\bar t\sum \limits_{i=1}^7y_i=40.17-4\times 9.32=2.89,\]所以\[r=\frac{\sum\limits_{i=1}^{7}{\left(t_i-\bar t\right)\left(y_i-\bar y\right)}}{\sqrt{\sum\limits_{i=1}^{7}{{{\left( {{t}_{i}}-\bar{t} \right)}^{2}}}}\sqrt{\sum\limits_{i=1}^{7}{{{\left( {{y}_{i}}-\bar{y} \right)}^{2}}}}}\approx 0.99,\]因为 $y$ 与 $t$ 的相关系数近似值为 $0.99$,说明 $y$ 与 $t$ 的线性相关程度相当高,从而可以用线性回归模型拟合 $y$ 与 $t$ 的关系.
-
建立 $y$ 关于 $t$ 的回归方程(系数精确到 $0.01$),预测 $2016$ 年我国生活垃圾无害化处理量.标注答案回归方程为 $\hat y=0.92+0.10 t$,预测 $2016$ 年我国生活垃圾无害化处理量约为 $1.82$ 亿吨解析考查线性回归方程的简单应用,根据公式计算即可.计算可得\[\hat{b}=\dfrac {\sum\limits_{i=1}^7 \left(t_i-\bar t\right)\left(y_i-\bar y\right)}{\sum\limits_{i=1}^{7}\left(t_i-\bar t\right)^2}\approx 0.103,\]所以\[\hat{a}=\bar{y}-\hat{b}\bar{t}\approx 0.92,\]所以回归方程为\[\hat y=0.10t+0.92,\]将 $2016$ 年对应的 $t=9$ 代入回归方程得 $\hat y=0.92+0.10\times 9=1.82$.
所以预测 $2016$ 年我国生活垃圾无害化处理量约为 $1.82$ 亿吨.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2