重置
序号 ID 年级 类型 来源 摘要 创建时间
20655 5c7769b4210b284290fc25f4 高中 解答题 自招竞赛 我们把具有如下性质的 $3\times 3$ 矩阵定义为“T-网格”：
（1）只有五个元素是1，其余的四个元素是0；
（2）三行、三列、两条主对角线（主对角线是 $\left\{ {{a}_{13}} ,{{a}_{22}}, {{a}_{31}} \right\}$ 和 $\left\{ {{a}_{11}}, {{a}_{22}}, {{a}_{33}} \right\}$）共八条线上至多只有一条线上的三个数是相等的。
求不同的“T-网格”的个数。		 2022-04-17 20:47:01
20630 5c8b1b3c210b286d07454113 高中 解答题 自招竞赛 称有序四元数组 $\left( a\text{,}b\text{,}c\text{,}d \right)$ 为有趣的，如果 $1\leqslant a\text{}b\text{}c\leqslant 10$，且 $a+d\text{}b+c$ 。求有趣的四元数组的个数。 2022-04-17 20:33:01
20614 5c8efe6f210b286d125ef320 高中 解答题 自招竞赛 九人围坐圆桌并有三道可选套餐。 $\text{3}$ 人选择牛肉套餐，$\text{3}$ 人选择鸡肉套餐，剩余三人选择鱼肉套餐。服务生按随机顺序上菜。求满足条件的上菜顺序，使得每个人都得到其所点套餐种类。 2022-04-17 20:25:01
20611 5c8efe9b210b286d07454181 高中 解答题 自招竞赛 在下图网络中的 $\text{16}$ 个圆中各站着一个学生。这 $\text{16}$ 名学生手中分发了 $\text{3360}$ 枚硬币。在同一时刻，每个学生将手中所有硬币平均传给所有与他相邻的人。传递玩硬币之后，每个学生手中的硬币数与开始相同。求站在最中心的学生一开始手中有多少硬币。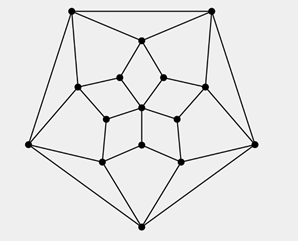 2022-04-17 20:22:01
20605 5c8efedd210b286d07454189 高中 解答题 自招竞赛 $n$ 名数学家坐在圆桌的 $n$ 个座位，顺时针编号依次为 $1\text{,}2\text{,}3\text{,}\cdots n$ 。休息之后他们再次落座，并且发现存在正整数 $a$ 满足：
（1）对于每个 $k$，之前坐在 $k$ 的数学家在休息过后坐在 $ka$（座位 $i+n$ 即为 $i$）
（2）对任意一对数学家，他们之间间隔的人数，无论是顺时针数还是逆时针数都与休息前间隔人数不同。
求所有可能的 $n$，$1<n<1000$		 2022-04-17 20:21:01
20552 5c944b55210b286d125ef552 高中 解答题 自招竞赛 亚伯粉刷房子需要 $15$ 小时，贝亚粉刷房子的速度比亚伯快 $50%$，科埃粉刷房子的速度是亚伯的两倍。开始粉刷时，亚伯先单独工作了 $1.5$ 小时；然后贝亚加入进来，两人一起工作；当房子的一半粉刷完时，科埃也加入进来，三人一起工作，直至房子粉刷完。求粉刷完这间房子共用了多少分钟时间 2022-04-17 20:50:00
20551 5c944b5a210b286d125ef557 高中 解答题 自招竞赛 阿诺德研究三种健康风险因子 $A,B,C$ 在男性人口中的流行性。在男性中随机选取一人，他仅有一种健康风险因子（但没有其他两种）的概率是 $0.1$；他仅有其中两种健康风险因子（但没有第三种）的概率是 $0.14$ 。在同时有 $A,B$ 两种健康风险因子的男性中，有三种健康风险因子的男性的比例是 $\frac{1}{3}$ 。在没有健康风险因子 $A$ 的男性中，没有这三种健康风险因子的男性比例是 $\frac{p}{q}$，其中 $p\text{,}q$ 是互质的正整数。求 $p+q$ 的值 2022-04-17 20:50:00
20534 5c9492de210b286d07454370 高中 解答题 自招竞赛 Steve对Jon说：“我想到一个所有根都是正整数的多项式。该多项式形如 $P\left( x \right)\text{=}2{{x}^{3}}-2a{{x}^{2}}+\left( {{a}^{2}}-81 \right)x-c$，其中 $a\text{,}c$ 是正整数。你能求出 $a\text{,}c$ 的值么？”Jon计算了一段时间后回复道，“满足条件的多项式不唯一。”Steve说：“你说的没错，这个是 $a$ 的值，”他给Jon写下一个正整数，“现在你能说出 $c$ 的值了吗？”Jon说：“现在 $c$ 还是有两种可能。”求 $c$ 的两种可能值之和。 2022-04-17 20:41:00
20530 5c949308210b286d125ef5dd 高中 解答题 自招竞赛 称 $\text{1}\text{2}\cdots \text{,}n$ 的一个排列 ${{a}_{1}}\text{,}{{a}_{2}}\text{,}\cdots {{a}_{k}}$ 是类上升的如果 ${{a}_{k}}\leqslant {{a}_{k+1}}+2\left( 1\leqslant k\leqslant n-1 \right)$ 。例如 $54321$ 和 $14253$ 都是 $1\text{,}2\text{,}3\text{,}4\text{,}5$ 的类上升排列，但 $45123$ 不是。求 $1\text{,}2\text{,}3\text{,}4\text{,}5\text{,}6\text{,}7$ 的类上升排列数 2022-04-17 20:38:00
20528 5c949315210b286d07454382 高中 解答题 自招竞赛 由字母 $A,B$ 构成的 $10$ 位数字符串有 ${{2}^{10}}\text{=}1024$ 种。求不含超过三个连续相同字母的字符串的个数 2022-04-17 20:37:00
20468 5c987b7d210b280b2256bf3f 高中 解答题 自招竞赛 两个各面标记为 $1\text{,}2\text{,}3\text{,}4\text{,}5\text{,}6$ 的普通骰子各面比重不同，其中标记数字为 $k$ 的面的概率比重为 $k$ 。用这样一对骰子扔出数字和为 $7$ 的概率为 $\frac{m}{n}$，其中 $m\text{,}n$ 为互质的正整数。求 $m+n$ 2022-04-17 20:05:00
20467 5c987b84210b280b2397e874 高中 解答题 自招竞赛 正二十面体每个面均为正三角形，每个顶点有 $5$ 个正三角形面交于此。该正二十面体如下图摆放，与最顶端顶点相邻的五个顶点构成的五棱柱的底面和与最下端顶点相邻的五个顶点构成的五棱柱的底面均与地面平行。求从顶端顶点到底部顶点的路径数，满足该路径上每一小段（即从正二十面体的一条棱）要么向下要么水平且没有经过重复顶点。 2022-04-17 20:04:00
20457 5c987bc4210b280b2397e89c 高中 解答题 自招竞赛 在坐标网格中，以每个格点为中心各有一个半径 $\frac{1}{10}$ 的圆和一个边长 $\frac{1}{5}$ 的正方形（各边平行于坐标轴）。端点为 $\left( 0\text{,}0 \right)\text{,}\left( 1001\text{,}429 \right)$ 的线段穿过了 $m$ 个正方形和 $n$ 个圆。求 $m+n$ 2022-04-17 19:58:59
20444 5c9996c7210b280b2397e8fc 高中 解答题 自招竞赛 将 $1\text{,}2\text{,}\cdots \text{,}9$ 排成 $3\times 3$ 的形式。对每个排列方式，${{a}_{1}}\text{,}{{a}_{2}}\text{,}{{a}_{3}}$ 分别为 $1\text{,}2\text{,}3$ 行的中位数，$m$ 为 $\left\{ {{a}_{1}}\text{,}{{a}_{2}}\text{,}{{a}_{3}} \right\}$ 的中位数。 $Q$ 为满足 $m\text{=}5$ 的排列的个数。求 $Q$ 模 $1000$ 的值 2022-04-17 19:50:59
20429 5c99ef65210b280b2397e973 高中 解答题 自招竞赛 五个小镇被道路网连接，每两个小镇之间恰好有一条路。现给每条路都指定单一方向，求满足条件的指派数，使得任意两个起点、终点小镇之间都存在道路联通（可以经过其它小镇） 2022-04-17 19:43:59
20426 5c99ef78210b280b2256c01d 高中 解答题 自招竞赛 $10\times 10\times 10$ 的格点网络包含了所有空间坐标系中形如 $\left( i\text{,}j\text{,}k \right)\left( 1\leqslant i\text{,}j\text{,}k\leqslant 10 \right)$ 的点。求恰好包含其中 $8$ 个点的直线的个数 2022-04-17 19:41:59
20424 5c9c2c4d210b280b2397e9d6 高中 解答题 自招竞赛 $S$ 是满足条件的有序数对 $\left( a,b \right)$ 的个数，其中 $\text{0}\leqslant a\leqslant 100,b\geqslant 0$，且 ${{x}^{2}}+ax+b$ 可分解为两个整系数一次多项式的乘积。求 $S$ 模 $1000$ 的值 2022-04-17 19:40:59
20414 5c9c2cb7210b280b2256c0a5 高中 解答题 自招竞赛 对 $U\text{=}\left\{ 1\text{,}2\text{,}3\text{,}\cdots \text{,}18 \right\}$ 的每个子集 $T$，$s\left( T \right)$ 是其所有元素之和，并且定义 $s\left( 0 \right)\text{=}0$ 。从 $U$ 的所有子集中随机选取子集 $T$，$s\left( T \right)$ 是 $3$ 的倍数的概率为 $\frac{m}{n}$，其中 $m\text{,n}$ 是互质的正整数。求 $m+n$ 2022-04-17 19:35:59
20412 5c9c2cc5210b280b2397ea02 高中 解答题 自招竞赛 一只青蛙从七边形 $S{{P}_{1}}{{P}_{2}}{{P}_{3}}E{{P}_{4}}{{P}_{5}}$ 的顶点 $S$ 出发。对七边形除了 $E$ 之外的每个顶点，青蛙每步都可以向其任一相邻顶点跳。当到达 $E$ 时，青蛙便停在原地。求满足条件的不同的跳跃序列数，使得青蛙不超过 $12$ 步到达点 $E$ 2022-04-17 19:34:59
20404 5c9c34cc210b280b2397ea49 高中 解答题 自招竞赛 一只青蛙在坐标平面的原点。从点 $\left( x\text{,}y \right)$ 出发，青蛙可以跳到 $\left( x+1\text{,}y \right)\text{,}\left( x+2\text{,}y \right)\text{,}\left( x\text{,}y+1 \right)\text{,}\left( x\text{,}y+2 \right)$ 四点中的任一点。求起点为 $\left( \text{0,0} \right)$ 终点为 $\left( \text{4,4} \right)$ 的不同的跳跃序列数 2022-04-17 19:29:59
0.169031s