在下图网络中的 $\text{16}$ 个圆中各站着一个学生。这 $\text{16}$ 名学生手中分发了 $\text{3360}$ 枚硬币。在同一时刻,每个学生将手中所有硬币平均传给所有与他相邻的人。传递玩硬币之后,每个学生手中的硬币数与开始相同。求站在最中心的学生一开始手中有多少硬币。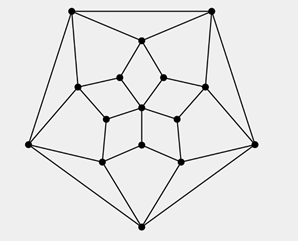

【难度】
【出处】
2012年第30届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
280
【解析】
设在中心的学生开始有 $a$ 个硬币,与他相临的学生开始有 $b$ 个硬币,生于学生一开始有 $c$ 个硬币。则手中有 $a$ 个硬币的学生各与 $5$ 个人相邻,手中有 $b$ 个硬币的学生各与 $3$ 个人相邻,手中有 $c$ 个硬币的学生各与 $4$ 个人相邻。因为交换之后每个人手中的硬币数不变,所以有 $a\text{=}5\cdot\frac{b}{3}\text{,}b\text{=}\frac{a}{5}+2\cdot\frac{c}{4}\text{,}c\text{=}2\cdot \frac{c}{4}+2\cdot \frac{b}{3}$,且有 $a+5b+10c\text{=}3360$ 。解得 $a\text{=}\frac{3360}{12}\text{=}280$
答案
解析
备注