阿诺德研究三种健康风险因子 $A,B,C$ 在男性人口中的流行性。在男性中随机选取一人，他仅有一种健康风险因子（但没有其他两种）的概率是 $0.1$；他仅有其中两种健康风险因子（但没有第三种）的概率是 $0.14$ 。在同时有 $A,B$ 两种健康风险因子的男性中，有三种健康风险因子的男性的比例是 $\frac{1}{3}$ 。在没有健康风险因子 $A$ 的男性中，没有这三种健康风险因子的男性比例是 $\frac{p}{q}$，其中 $p\text{,}q$ 是互质的正整数。求 $p+q$ 的值
【难度】
【出处】
2014年第32届美国数学邀请赛Ⅱ（AIMEⅡ）
【标注】
【答案】
075
【解析】
我们不妨假设总人数为 $100$ 。则根据条件可作如下韦恩图。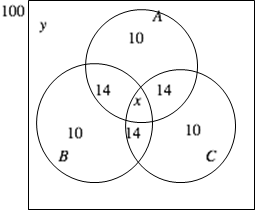
设有三种致病因素的人数为 $x$ 。则根据条件，$x\text{=}\frac{1}{3}\left( x+14 \right)\Rightarrow x\text{=}7$ 。设没有致病因素的人数为 $y$ 。则 $y\text{=}100-3\cdot10-3\cdot 14-7\text{=}21$ 。具有致病因素 $A$ 的人数为 $10+2\cdot 14+7\text{=}45$，则不含致病因素 $A$ 的人数为 $100-45\text{=}55$ 。于是所求比例为 $\frac{21}{55}$ 。所求值为 $21+55\text{=}075$
设有三种致病因素的人数为 $x$ 。则根据条件，$x\text{=}\frac{1}{3}\left( x+14 \right)\Rightarrow x\text{=}7$ 。设没有致病因素的人数为 $y$ 。则 $y\text{=}100-3\cdot10-3\cdot 14-7\text{=}21$ 。具有致病因素 $A$ 的人数为 $10+2\cdot 14+7\text{=}45$，则不含致病因素 $A$ 的人数为 $100-45\text{=}55$ 。于是所求比例为 $\frac{21}{55}$ 。所求值为 $21+55\text{=}075$
答案
解析
备注
