一只青蛙从七边形 $S{{P}_{1}}{{P}_{2}}{{P}_{3}}E{{P}_{4}}{{P}_{5}}$ 的顶点 $S$ 出发。对七边形除了 $E$ 之外的每个顶点，青蛙每步都可以向其任一相邻顶点跳。当到达 $E$ 时，青蛙便停在原地。求满足条件的不同的跳跃序列数，使得青蛙不超过 $12$ 步到达点 $E$
【难度】
【出处】
2018年第36届美国数学邀请赛Ⅰ（AIMEⅠ）
【标注】
【答案】
351
【解析】
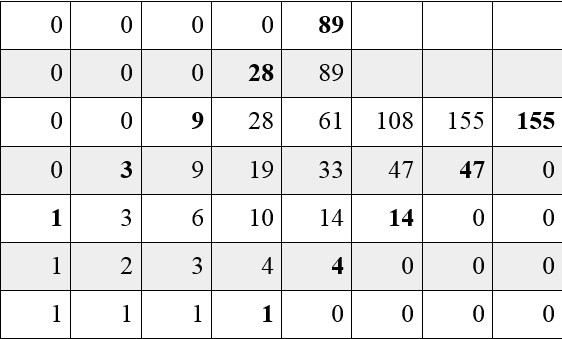
我们递推归纳计算。为方便起见，我们假设七个顶点在一条直线上 $E\leftrightarrow{{P}_{4}}\leftrightarrow {{P}_{5}}\leftrightarrow S\leftrightarrow{{P}_{1}}\leftrightarrow {{P}_{2}}\leftrightarrow {{P}_{3}}\leftrightarrow E$，于是每步的选择为左／右。我们计算长度小于 $11$、起点为 $S$ 终点为 ${{P}_{4}},{{P}_{3}}$ 的路径数。我们用二维格点赋值的方式计算，起点为 $\left(0,0 \right)$，向右走一步对应沿 $x$ 轴正方向走一步，向左走一步对应沿 $y$ 轴正方向走一步。因为我们不想向左超过两步或向右超过三步，所以我们的路径不能穿过 $y\text{=}x+2\text{,}y\text{=}x-3$ 。令 $p\left(x\text{,}y \right)$ 表示从 $\left( 0\text{,}0 \right)$ 到 $\left( x\text{,}y \right)$ 的路径数。初始条件有 $p\left(x\text{,}0 \right)\text{=}\left\{ \begin{matrix}1\text{,}x\leqslant 3 \\
0\text{,}x\text{}3 \\
\end{matrix} \right.$，$p\left( 0,y \right)=\left\{ \begin{matrix}1,y\leqslant 2 \\
0,y>2 \\
\end{matrix}\right.$，递推关系为 $p\left( x\text{,}y \right)\text{=}p\left( x-1\text{,}y\right)+p\left( x\text{,}y-1 \right)x\text{,}y\geqslant 1$ 。于是我们可以得到以下赋值表，左下角对应原点。加粗的部分表示从 $S$ 出发 $2\text{,}4\text{,}6\text{,}8\text{,}10$ 步到达 ${{P}_{4}}$ 的路径数和从 $S$ 出发 $3\text{,}5\text{,}7\text{,}9\text{,}11$ 步到达 ${{P}_{3}}$ 的路径数，于是一共有 $1+3+9+28+89+1+4+14+47+155\text{=}351$ 步
答案
解析
备注
