重置
序号 ID 年级 类型 来源 摘要 创建时间
20791 5c74ea1b210b28428f14cc26 高中 解答题 自招竞赛 一副纸牌由 $n$ 张不同的卡片组成，其中 $n\in Z$ 且 $n\geqslant 6$，从这副纸牌里取出6张卡片的方法数是取出3张卡片的方法数的6倍，试求 $n$ 。 2022-04-17 20:03:03
20790 5c74ea24210b284290fc23d4 高中 解答题 自招竞赛 一家饭店正为3位顾客打包早餐，每一份早餐包括3种夹心，分别是坚果、奶酪和水果的卷饼，店员将9个卷饼独立包装，在全部包装后无法区分卷饼的种类，她随机将卷饼3个3个放入袋子中交给顾客，设每位顾客均得到三种不同种类卷饼的概率为 $\frac{m}{n}$，其中 $m$，$n$ 是互素的正整数，试求 $m+n$ 。 2022-04-17 20:03:03
20761 5c75f0c1210b28428f14ccc4 高中 解答题 自招竞赛 求满足如下条件的 $\left( 1, 2 ,3 ,\ldots ,12 \right)$ 的排列 $\left( {{a}_{1}}, {{a}_{2}} ,{{a}_{3}}, \ldots, {{a}_{12}} \right)$ 的个数
${{a}_{1}}>{{a}_{2}}>{{a}_{3}}>{{a}_{4}}>{{a}_{5}}>{{a}_{6}}$，${{a}_{6}}<{{a}_{7}}<{{a}_{8}}<{{a}_{9}}<{{a}_{10}}<{{a}_{11}}<{{a}_{12}}$ 。
例如，$\left( 6, 5, 4, 3, 2, 1, 7, 8, 9, 10, 11, 12 \right)$ 就是一个满足上述条件的排列		 2022-04-17 20:46:02
20760 5c75f0cb210b28428f14ccc9 高中 解答题 自招竞赛 一个骰子的六个面分别标有数1，2，3，4，5，6，其中相对的两个面的数字和为7。掷一次此骰子时，出现某个面 $F$ 的概率大于 $\frac{1}{6}$，出现与 $F$ 相对的面的概率小于 $\frac{1}{6}$，出现其余各面的概率均为 $\frac{1}{6}$ 。已知将此骰子连续扔两次，出现两面的数字和为7的概率是 $\frac{47}{288}$ 。设扔一次出现 $F$ 面的概率是 $\frac{m}{n}$，其中 $m n$ 为互素的正整数，试求 $m+n$ 的值。 2022-04-17 20:45:02
20757 5c75f0ef210b284290fc248b 高中 解答题 自招竞赛 如图所示将多个全等的正三角形涂上6种颜色，每种颜色的三角形都有很多个。现将四个正三角形拼成一个大的正三角形，能得到多少种不同的大正三角形？（若将大三角形经过旋转或翻转、对称与另一大三角形颜色完全一致，则算同一种。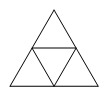） 2022-04-17 20:44:02
20756 5c75f0fa210b28428f14ccd5 高中 解答题 自招竞赛 圆 ${{C}_{1}} {{C}_{2}} {{C}_{3}}$ 的圆心分别为 $\left( 0 ,0 \right) \left( 12 ,0 \right) \left( 24, 0 \right)$，它们的半径分别为 $1 ,2, 4$ 。直线 ${{t}_{1}}$ 是圆 ${{C}_{1}}$ 和 ${{C}_{2}}$ 的斜率为正的内公切线，直线 ${{t}_{2}}$ 是圆 ${{C}_{2}}$ 和 ${{C}_{3}}$ 的斜率为负的内公切线，设直线 ${{t}_{1}}$ 和 ${{t}_{2}}$ 交于点 $\left( x,y \right)$，且 $x=q-p\sqrt{r}$，其中 $p ,q ,r$ 为正整数，且 $r$ 不能被任何素数的平方整除。试求 $p+q+r$ 的值。 2022-04-17 20:43:02
20755 5c75f103210b28428f14ccdb 高中 解答题 自招竞赛 有七支球队进行足球锦标赛，每一个球队与其他各球队都恰比赛一场。每场球赛都分出胜负，每两队之间胜负的概率都是50%，没有平局，胜者得1分，负者得0分。各场球赛的结果都是互相独立的，以各队得分的总和排定各队的名次。若锦标赛第一轮 $A$ 队胜了 $B$ 队，则比赛结束后、$A$ 队积分比 $B$ 队高的概率 $\frac{m}{n}$，其中 $m n$ 为互素的正整数，试求 $m+n$ 的值。 2022-04-17 20:43:02
20738 5c75ffd1210b284290fc24d2 高中 解答题 自招竞赛 某数学学会发行一套纪念牌，每块纪念牌上包含由 $5$ 个符号组成的数列，这 $5$ 个符号选自AIME中的字母和 $2007$ 中的数码，且同一个符号在数列中出现的次数不超过它在“$\text{AIME}2007$”中出现的次数。这套纪念牌共包含 $N$ 块，每种可能出现的数列恰出现一次。试求 $\frac{N}{10}$ 。 2022-04-17 20:34:02
20716 5c761aa6210b284290fc2518 高中 解答题 自招竞赛 考查完全由字母 $A$ 和 $B$ 组成的具有如下性质的序列：每段连续的 $A$ 有偶数个，每段连续的 $B$ 有奇数个．例如 $AA$，$B$，$AABAA$ 都是这样的序列，而 $BBAB$ 就不是这样的序列．
在长度为14的序列中有多少个具有这种性质？		 2022-04-17 20:21:02
20709 5c761fe2210b28428f14cdb8 高中 解答题 自招竞赛 一块长方体奶酪的长、宽、高分别为 $10\text{cm}$，$13\text{cm}$，$14\text{cm}$．每次从平行于奶酪某个面的方向中切出厚度为 $1\text{cm}$ 的一片奶酪，共切10次，每次切的方向不必是互相平行的．在10次切除之后剩余奶酪的最大体积是多少立方厘米？ 2022-04-17 20:17:02
20701 5c762097210b28428f14cddc 高中 解答题 自招竞赛 有两根不同的旗杆和19面旗帜，其中蓝旗有10面，绿旗有9面．现在要将所有旗帜都挂在旗杆上，使得每一根旗杆至少有1面旗帜，且任意两面绿旗不相邻．设这样的排列方法数为 $N$，求 $N$ 除以1000的余数． 2022-04-17 20:12:02
20697 5c763c13210b28428f14ce00 高中 解答题 自招竞赛 抛掷一枚硬币，其正面朝上的概率为 $p$，反面朝上的概率为 $1-p$，拋掷硬币8次，每次拋掷互相独立．设出现“3正5反”的概率恰好是出现“5正3反”的概率的 $\frac{1}{25}$，设 $p=\frac{m}{n}$（$m$，$n$ 是互素的正整数），求 $m+n$． 2022-04-17 20:10:02
20693 5c763c41210b28428f14ce21 高中 解答题 自招竞赛 一项比赛给参赛者提供 $A$，$B$，$C$ 三项奖金，每项奖金的数额是 $1\text{ }\!\!\tilde{ }\!\!\text{ }9999$ 美元之间的整数（包括1美元和9999美元，不同项目的奖金数额可能相等）．参赛者必须依次猜出 $A$，$B$，$C$ 三项奖金的数额才可获奖．作为提示，三项奖金所包含的所有数字会被给出．某一天给出的提示数字是1，1，1，1，3，3，3．请根据提示的数字，求出三项奖金数额的所有可能情形的总数． 2022-04-17 20:07:02
20692 5c763c4c210b284290fc2562 高中 解答题 自招竞赛 每年一届的行星数学邀请赛由5名火星人、5名金星人、5名地球人组成的委员会命题．开会时，委员会成员围着配有15张椅子并顺时针编号 $1\text{ }\!\!\tilde{ }\!\!\text{ }15$ 的圆桌坐下．委员会的规则要求1号椅子必须坐火星人，15号椅子必须坐地球人，且地球人不能坐在火星人的左邻，火星人不能坐在金星人的左邻，金星人不能坐在地球人的左邻．委员会安排座位的所有可能的方法总数是 $N\cdot {{\left( 5! \right)}^{3}}$，求 $N$ 。 2022-04-17 20:06:02
20684 5c774284210b28428f14ce4b 高中 解答题 自招竞赛 前14个正整数组成一个集合 $\left| 1, 2,3, \ldots ,14 \right|$．此集合的符合如下条件的子集的数目为 $m$：子集均含有5个元素，且这5个元素至少有两个是连续的，求 $m$ 除以 $1000$ 的余数． 2022-04-17 20:03:02
20683 5c774290210b28428f14ce56 高中 解答题 自招竞赛 Dave投掷一颗均匀的骰子，直到第一次出现6点为止；Linda也独立投掷―颗均匀的骰子，直到第一次出现6点为止．设Dave投掷的次数等于或与Linda投掷的次数相差不超过1的概率为 $\frac{m}{n}$（其中 $m$，$n$ 是互素的正整数、求 $m+n$． 2022-04-17 20:02:02
20680 5c7742b0210b28428f14ce6b 高中 解答题 自招竞赛 设 $A$、$B$ 是半径为2的半圆弧的两端点．该半圆被六个点 ${{C}_{1}}$，${{C}_{2}}$，…，${{C}_{6}}$ 等分成七段，连接所有的弦 $A{{C}_{i}}$ 和 $B{{C}_{i}}$．设 $n$ 是这12条弦长度的乘积，求 $n$ 除以1000的余数． 2022-04-17 20:01:02
20661 5c776989210b284290fc25d7 高中 解答题 自招竞赛 Dave抵达一个机场，该机场有 $12$ 个安检门，它们排成一条直线，相邻的两个安检门的间距都是100英尺。他的安检门是随机指派的。在某个安检门等待一会之后，Dave被告知他的安检门已更换，新的安检门也是随机指派的。设Dave步行到新的安检门的路程小于或等于400英尺的概率是 $\frac{m}{n}$，其中 $m$，$n$ 是互素的正整数，求 $m+n$ 的值。 2022-04-17 20:51:01
20653 5c7769c0210b28428f14ceef 高中 解答题 自招竞赛 一副纸牌有52张，分别编号为1，2，3，…，52。 $A$，$B$，$C$，$D$ 四个人每人从中抽出一张，不放回。每张纸牌被抽到的可能性是相同的。抽到编号较小的两人为一个组，抽到编号较大的两个人为另一组。已知 $A$ 抽到编号为 $a$，$a+9$ 的两张纸牌中的一张，而 $D$ 抽到这两张纸牌中的另一张，设 $A$，$D$ 两个人在同一组的概率为 $p\left( a \right)$ 。当 $p\left( a \right)\geqslant \frac{1}{2}$ 时，$p\left( a \right)$ 的最小值为 $\frac{m}{n}$，其中 $m$，$n$ 是互素的正整数。求 $m+n$ 的值。 2022-04-17 20:46:01
20629 5c8b1b43210b286d125ef28f 高中 解答题 自招竞赛 爱德有 $5$ 块相同的绿色大理石和大量相同的红色大理石。将绿色和红色的大理石排成一排后，他发现与自己右侧相邻石子颜色相同的大理石和与自己右侧相邻石子颜色不同的大理石个数相同。例如，排列方式为 绿绿红红红绿绿红绿 既满足条件。记 $m$ 为存在满足条件的排列方式的红大理石数目的最大值，并记 $N$ 为 $m+5$ 块大理石构成的满足条件的排列方式的个数。求 $N$ 模 $1000$ 的值。 2022-04-17 20:32:01
0.175365s