设 $A$、$B$ 是半径为2的半圆弧的两端点.该半圆被六个点 ${{C}_{1}}$,${{C}_{2}}$,…,${{C}_{6}}$ 等分成七段,连接所有的弦 $A{{C}_{i}}$ 和 $B{{C}_{i}}$.设 $n$ 是这12条弦长度的乘积,求 $n$ 除以1000的余数.
【难度】
【出处】
2009年第27届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
672
【解析】
如图所示,在复平面上画出半圆弧使得 $A$,位于 $-2$,而 $B$ 位于 $2 $,则这个圆弧恰好是以 $0 $ 为圆心半径为 $2 $ 的圆的一半,且这 $12 $ 条弦分别等于 $A{{C}_{1}}$,$A{{C}_{2}}$,…,$A{{C}_{6}}$,$A{{C}_{7}}$,…,$A{{C}_{11}}$,$AC12$,其中的点 ${{C}_{7}}$,…,${{C}_{11}}$,${{C}_{12}}$ 分别是 ${{C}_{1}}$,${{C}_{2}}$,…,${{C}_{6}}$ 关于实轴的对称点,则14个点 $A$,$B$,${{C}_{1}}$,${{C}_{2}}$,…,${{C}_{6}}$,${{C}_{7}}$,…,${{C}_{11}}$,${{C}_{12}}$ 恰好是 ${{2}^{14}}$ 的14个根.点 $z$ 到点2之间的弦长等于复数 $\omega=z-2$ 的模,每一个复数 $\omega$ 都满足 ${{\left(\omega +2 \right)}^{14}}={{2}^{14}}$.这12条弦的长度的乘积与 $AB$ 相乘的结果等于方程 $\frac{{{\left(\omega +2 \right)}^{14}}-{{2}^{14}}}{\omega }=0$ 的所有根的乘积的模.将这个方程的左边化为多项式后,所有根的乘积是这个多项式的常数项.由二项式定理,这个常数项应等于 $C_{14}^{13}\cdot {{2}^{13}}$,它等于 $AB\cdot n$.而 $AB=4$,所以 $n=\frac{14\cdot {{2}^{13}}}{4}=14\cdot{{2}^{11}}=28672$,故所要求的结果为672.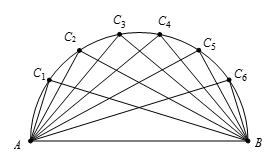

答案
解析
备注