如图所示将多个全等的正三角形涂上6种颜色,每种颜色的三角形都有很多个。现将四个正三角形拼成一个大的正三角形,能得到多少种不同的大正三角形?(若将大三角形经过旋转或翻转、对称与另一大三角形颜色完全一致,则算同一种。)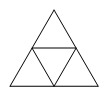

【难度】
【出处】
2006年第24届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
336
【解析】
因为一个大三角形顶点间的任意变换都可以通过旋转或对称得到,因此大三角形的颜色取决于两点,其一是角落上三个小三角形使用颜色组合,其二位于中心上的小三角形使用的颜色。如果角落上三个小三角形颜色相同,那么它们有六种可能的颜色组合;如果角落上三个小三角形恰好有两个颜色相同,那么它们有 $6\times 5\text{=}30$ 种颜色组合;如果角落上三个小三角形的颜色互不相同,那么它们有 $\text{C}_{6}^{3}=20$ 种颜色组合所以角落上三个小三角形的颜色组合一共有 $6+30+20=56$ 种。因为位于中心的小三角形的颜色有6种选择,所以不同的大三角形一共有 $6\times 56=336$ 种。
答案
解析
备注