重置
序号 ID 年级 类型 来源 摘要 创建时间
20624 5c8b1b60210b286d07454123 高中 解答题 自招竞赛 现有三个不同国家，每个国家三人共九名代表。他们随机坐在圆桌的九个座位。记每个代表至少与一名来自不同国家代表相邻的概率为 $\frac{m}{n}$，其中 $m\text{,}n$ 为互质正整数。求 $m+n$ 。 2022-04-17 20:30:01
20602 5c8f565a210b286d074541c3 高中 解答题 自招竞赛 某大学数学科学学院有数学部、统计学部和信息科学部三个部门。每个部门分别有男女各两名教授。委员会由三男三女共六名教授组成，同时必须满足每个部门均有两名教授在委员会中。求满足条件的委员会组成数。 2022-04-17 20:19:01
20593 5c8f569c210b286d074541ef 高中 解答题 自招竞赛 现有一九人组，其中每人均与组中其他两人握手。记 $N$ 为可能存在的握手方式总数。我们认定两个握手方式是不同的当且仅当至少有两人仅在其中一种方式下握了手。求 $N$ 模 $1000$ 的值。 2022-04-17 20:15:01
20588 5c90872c210b286d125ef3d9 高中 解答题 自招竞赛 在下图所示的 $13$ 个正方形中，$8$ 个正方形被染成红色，剩余 $5$ 个被染成蓝色。随机从所有可能的染色方案中选取一种，将其绕中心的正方形旋转 ${{90}^{{}^\circ }}$ 后所得染色方式相同的概率为 $\frac{1}{n}$ 。求 $n$ 2022-04-17 20:13:01
20586 5c908736210b286d125ef3e3 高中 解答题 自招竞赛 Melinda有三个空盒子和 $12$ 本教材，其中三本为数学书。三个盒子中分别用来装 $3\text{,}4\text{,}5$ 本她的教材。如果Melinda随机把书装入盒子中，三本数学书在同一盒子的概率为 $\frac{m}{n}$，其中 $m\text{,}n$ 为互质正整数。求 $m+n$ 2022-04-17 20:12:01
20580 5c90875e210b286d125ef400 高中 解答题 自招竞赛 $\Delta A{{B}_{0}}{{C}_{0}}$ 中，$A{{B}_{0}}=12,{{B}_{0}}{{C}_{0}}=17,{{C}_{0}}A=25$ 。对每个正整数 $n$，${{B}_{n}}\text{,}{{C}_{n}}$ 分别在 $A{{B}_{n-1}}\text{,}A{{C}_{n-1}}$ 上，且满足 $\Delta A{{B}_{n}}{{C}_{n}}-\Delta {{B}_{n-1}}{{C}_{n}}{{C}_{n-1}}-\Delta A{{B}_{n-1}}{{C}_{n-1}}$ 。所有 $\Delta {{B}_{n-1}}{{C}_{n}}{{B}_{n}}\left( n\geqslant 1 \right)$ 的并集覆盖的面积可表示为 $\frac{p}{q}$，其中 $p\text{,}q$ 为互质正整数。求 $q$ 2022-04-17 20:07:01
20579 5c908883210b286d125ef40b 高中 解答题 自招竞赛 $N$ 为满足下述条件的有序三元数组 $\left( A,B,C \right)$ 的个数。（a）$0\leqslant A<B<C\leqslant 99$，（b）存在整数 $a\text{,}b\text{,}c$ 和质数 $p$ 满足 $0\leqslant b\text{}a\text{}c\text{}p$，（c）$p$ 整除 $A-a\text{,}B-b\text{,}C-c$，（d）$\left( A\text{,}B\text{,}C \right)\left( b\text{,}a\text{,}c \right)$ 构成等差数列。求 $N$ 2022-04-17 20:07:01
20571 5c91ccf7210b286d0745426d 高中 解答题 自招竞赛 一个 $7\times 1$ 的板子被型如 $m\times 1$ 的瓷砖无重叠覆盖。每块瓷砖可以覆盖任意数目相邻的正方形，并且每块瓷砖完全落在板上。瓷砖的颜色可为红蓝绿。 $N$ 为整块板子所用瓷砖包含了红蓝绿三种颜色的覆盖方案数。例如，依次用 $1\times 1$ 的红瓷砖，$2\times 1$ 的绿瓷砖，$1\times 1$ 的绿瓷砖，$2\times 1$ 的蓝瓷砖，$1\times 1$ 的绿瓷砖各一块的方案及满足条件。求 $N$ 模 $1000$ 的值 2022-04-17 20:02:01
20564 5c9308ae210b286d125ef4ad 高中 解答题 自招竞赛 一个容器中有四个绿球和 $6$ 个蓝球。另一个容器中有 $16$ 个绿球和 $N$ 个蓝球。从两容器中各随机取出一球，两球颜色相同的概率为 $0.58$ 。求 $N$ 2022-04-17 20:57:00
20557 5c9308e3210b286d125ef4ce 高中 解答题 自招竞赛 一标记从坐标网格的原点 $\left( 0\text{,}0 \right)$ 出发连续移动六步，每步都沿平行于坐标轴方向且移动距离为 $1$ 。每步都等可能的沿四个方向之一且步与步之间相互独立。六步之后标记落在 $\left| y \right|\text{=}\left| x \right|$ 的图像上的概率为 $\frac{m}{n}$，其中 $m\text{,}n$ 为互质正整数。求 $m+n$ 2022-04-17 20:53:00
20547 5c944b70210b286d125ef56e 高中 解答题 自招竞赛 查尔斯有两颗六面骰子，其中一个骰子是质地均匀的，另一个骰子不均匀，质地不均匀的骰子抛一次，出现 $6$ 的概率是 $\frac{p}{q}$，其中 $p\text{,}q$ 是互质的正整数。求 $p+q$ 的值 2022-04-17 20:48:00
20544 5c944b7f210b286d07454321 高中 解答题 自招竞赛 将 $10$ 把一字排成一圈，从中选出若干把椅子，若选出的椅子中至少有三把相邻，求不同选法的种数。 2022-04-17 20:47:00
20541 5c944b96210b286d07454327 高中 解答题 自招竞赛 有 $10$ 个大人进去一个房间，脱下他们的鞋，扔成一堆，过了一会儿，进来一个小孩，随即把左脚的鞋与右脚的鞋配成一双，在配对过程中，不考虑这两只鞋是否是原来的一双。从小孩配对的 $10$ 双鞋中，对小于 $5$ 的一切正整数 $k$，不存在 $k$ 双鞋恰好是其中 $k$ 个人的鞋。这种情况发生的概率是 $\frac{m}{n}$，其中 $m\text{,}n$ 是互质的正整数。求 $m+n$ 的值 2022-04-17 20:45:00
20535 5c9492d8210b286d125ef5d0 高中 解答题 自招竞赛 从 $n\times n$ 的正方形网格中随机选取两个单位正方形。求最小的正整数 $n$ 使得所选取的两个单位正方形水平或竖直方向相邻的概率小于 $\frac{1}{2015}$ 2022-04-17 20:41:00
20463 5c987ba3210b280b2256bf4c 高中 解答题 自招竞赛 对 $1\text{,}2\text{,}\cdots \text{,9}$ 的一重排列 $p\text{=}\left( {{a}_{1}}\text{,}{{a}_{2}}\text{,}\cdots \text{,}{{a}_{9}} \right)$，令 $s\left( p \right)$ 为三位数 $\overline{{{a}_{1}}{{a}_{2}}{{a}_{3}}},\overline{{{a}_{4}}{{a}_{5}}{{a}_{6}}}\text{,}\overline{{{a}_{7}}{{a}_{8}}{{a}_{9}}}$ 之和。 $m$ 为个位数字为 $0$ 的 $s\left( p \right)$ 的最小值。 $n$ 为满足 $s\left( p \right)\text{=}m$ 的排列 $p$ 的个数。求 $\left| m-n \right|$ 2022-04-17 20:02:00
20455 5c999682210b280b2256bf8a 高中 解答题 自招竞赛 $15$ 个不同的点在 $\Delta ABC$ 的边上：其中 $3$ 个为三角形的顶点 $A,B,C$，$3$ 个点在 $AB$ 上，$4$ 个在 $BC$ 上，$5$ 个在 $CA$ 上。求所有面积为正数的三角形的个数，其顶点在这 $15$ 个点中 2022-04-17 19:57:59
20439 5c99ef2b210b280b2397e950 高中 解答题 自招竞赛 求 $\left\{ 1\text{,}2\text{,}3\text{,}4\text{,}5\text{,}6\text{,}7\text{,}8 \right\}$ 满足下述条件的子集的个数：其既不是 $\left\{ 1\text{,}2\text{,}3\text{,}4\text{,}5 \right\}$ 子集，也不是 $\left\{ 4\text{,}5\text{,}6\text{,}7\text{,}8 \right\}$ 的子集 2022-04-17 19:48:59
20438 5c99ef32210b280b2256bff9 高中 解答题 自招竞赛 ${{T}_{1}},{{T}_{2}}\text{,}{{T}_{3}}\text{,}{{T}_{4}}$ 都是决赛的种子选手。在半决赛中 ${{T}_{1}}\text{,}{{T}_{4}}$ 进行比赛，${{T}_{2}}\text{,}{{T}_{3}}$ 进行比赛。两场比赛的胜者将在决赛中对战决出胜者。 ${{T}_{i}}\text{,}{{T}_{j}}$ 进行比赛时，${{T}_{i}}$ 赢得比赛的概率为 $\frac{i}{i+j}$，每场比赛的结果都是相互独立的。 ${{T}_{4}}$ 最终夺冠的概率为 $\frac{p}{q}$，其中 $p\text{,}q$ 是互质正整数。求 $p+q$ 2022-04-17 19:48:59
20431 5c99ef58210b280b2397e967 高中 解答题 自招竞赛 一副特殊的牌有 $49$ 张，共有七种颜色且每张牌上标记 $1-7$ 中的一个数字。每个数字-颜色组合恰好对应一张牌。Sharon从这副牌中随机选取一组 $8$ 张牌。已知她选出的这组牌中包含了所有数字和所有颜色，她从中随机扔掉一张后剩余七张牌还包含所有颜色和数字的概率为 $\frac{p}{q}$，其中是互质正整数。求 $p+q$ 2022-04-17 19:44:59
20428 5c99ef6c210b280b2256c011 高中 解答题 自招竞赛 圆 ${{C}_{0}}$ 半径为 $1$，${{A}_{0}}$ 是圆 ${{C}_{0}}$ 上一点。圆 ${{C}_{1}}$ 半径为 $r\left( r\text{}1 \right)$ 且与圆 ${{C}_{0}}$ 内切于 ${{A}_{0}}$ 。 ${{A}_{1}}$ 在圆 ${{C}_{1}}$ 上且为 ${{A}_{0}}$ 绕 ${{C}_{1}}$ 逆时针转 ${{90}^{{}^\circ }}$ 的对应点。圆 ${{C}_{2}}$ 半径为 ${{r}^{2}}$ 且与圆 ${{C}_{1}}$ 内切于 ${{A}_{1}}$ 。依此类推，得到一系列圆 ${{C}_{1}}\text{,}{{C}_{2}}\text{,}{{C}_{3}}\text{,}\cdots $ 和一系列对应圆周上的点 ${{A}_{1}},{{A}_{2}},{{A}_{3}},\cdots $，其中圆 ${{C}_{n}}$ 半径为 ${{r}^{n}}$，与圆 ${{C}_{n-1}}$ 内切于 ${{A}_{n-1}}$，${{A}_{n}}$ 在圆 ${{C}_{n}}$ 上且为 ${{A}_{n-1}}$ 绕 ${{C}_{n-1}}$ 逆时针转 ${{90}^{{}^\circ }}$ 的对应点（如下图所示）。存在在上述所有圆内的点 $B$ 。当 $r\text{=}\frac{11}{60}$，${{C}_{0}}$ 与 $B$ 之间的距离为 $\frac{m}{n}$，其中 $m\text{,}n$ 是互质正整数。求 $m+n$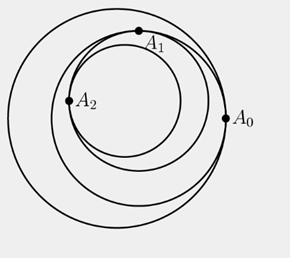 2022-04-17 19:42:59
0.557759s