圆 ${{C}_{0}}$ 半径为 $1$,${{A}_{0}}$ 是圆 ${{C}_{0}}$ 上一点。圆 ${{C}_{1}}$ 半径为 $r\left( r\text{}1 \right)$ 且与圆 ${{C}_{0}}$ 内切于 ${{A}_{0}}$ 。 ${{A}_{1}}$ 在圆 ${{C}_{1}}$ 上且为 ${{A}_{0}}$ 绕 ${{C}_{1}}$ 逆时针转 ${{90}^{{}^\circ }}$ 的对应点。圆 ${{C}_{2}}$ 半径为 ${{r}^{2}}$ 且与圆 ${{C}_{1}}$ 内切于 ${{A}_{1}}$ 。依此类推,得到一系列圆 ${{C}_{1}}\text{,}{{C}_{2}}\text{,}{{C}_{3}}\text{,}\cdots $ 和一系列对应圆周上的点 ${{A}_{1}},{{A}_{2}},{{A}_{3}},\cdots $,其中圆 ${{C}_{n}}$ 半径为 ${{r}^{n}}$,与圆 ${{C}_{n-1}}$ 内切于 ${{A}_{n-1}}$,${{A}_{n}}$ 在圆 ${{C}_{n}}$ 上且为 ${{A}_{n-1}}$ 绕 ${{C}_{n-1}}$ 逆时针转 ${{90}^{{}^\circ }}$ 的对应点(如下图所示)。存在在上述所有圆内的点 $B$ 。当 $r\text{=}\frac{11}{60}$,${{C}_{0}}$ 与 $B$ 之间的距离为 $\frac{m}{n}$,其中 $m\text{,}n$ 是互质正整数。求 $m+n$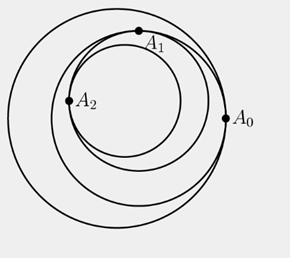

【难度】
【出处】
2017年第35届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
110
【解析】
令 ${{C}_{0}}$ 为原点,${{A}_{0}}$ 坐标为 $\left(1\text{,}0 \right)$ 建立平面直角坐标系。于是 ${{A}_{1}}\text{=}\left(1-r\text{,}r \right)\text{,}{{A}_{2}}\text{=}\left(1-r-{{r}^{2}}\text{,}r-{{r}^{2}} \right)\text{,}{{A}_{3}}\text{=}\left(1-r-{{r}^{2}}+{{r}^{3}}\text{,}r-{{r}^{2}}-{{r}^{3}}\right)\text{,}{{A}_{4}}\text{=}\left( 1-r-{{r}^{2}}+{{r}^{3}}+{{r}^{4}}\text{,}r-{{r}^{2}}-{{r}^{3}}+{{r}^{4}}\right)$ 。该点列极限点为 $B$,$B\text{=}\left(\frac{1-r}{{{r}^{2}}+1}\text{,}\frac{r-{{r}^{2}}}{{{r}^{2}}+1} \right)$ 。原点到 $B$ 的距离为 $\sqrt{{{\left(\frac{1-r}{\sqrt{{{r}^{2}}+1}} \right)}^{2}}+{{\left(\frac{r-{{r}^{2}}}{{{r}^{2}}+1} \right)}^{2}}}\text{=}\frac{1-r}{\sqrt{{{r}^{2}}+1}}$ 。代入 $r\text{=}\frac{11}{60}$ 得到距离为 $\frac{49}{61}$,故所求值为 $49+61\text{=}110$
答案
解析
备注