重置
序号 ID 年级 类型 来源 摘要 创建时间
18992 5d50d727210b280220ed78ae 高中 解答题 自招竞赛 在一个圆周上给定十二个红点，求 $n$ 的最小值，使得存在以红点为顶点的 $n$ 个三角形，满足：以红点为端点的每条弦．都是其中某个三角形的一条边． 2022-04-17 19:36:46
18988 5d511317210b280220ed7925 高中 解答题 自招竞赛 在 $8\times 8$ 方格表中，最少需要挖去几个小方格，才能使得无法从剩余的方格表中剪裁出一片形状如图所示完整的 $T$ 形五方连块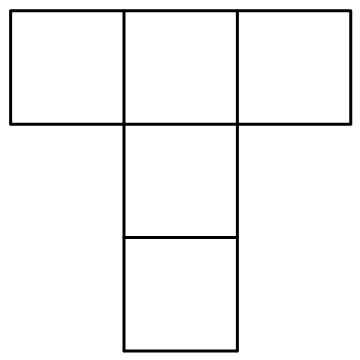？ 2022-04-17 19:34:46
18979 5d512540210b280220ed794e 高中 解答题 自招竞赛 已知集合 $S=\{1,2,3,\cdots,3n\}$，$n$ 是正整数，$T$ 是 $S$ 的子集，满足：对任意的 $x,y,z\in T$（其中 $x,y,z$ 可以相同）都有 $x+y+z\not\in T$，求所有这种集合 $T$ 的元素个数的最大值． 2022-04-17 19:29:46
18976 5d514546210b280220ed798d 高中 解答题 自招竞赛 设正整数 $m,n\geqslant 2$，对于任一个 $n$ 元整数集 $A=\{a_1,a_2,\cdots,a_n\}$，取每一对不同的数 $a_i,a_j(j>i)$，作差 $a_j-a_i$，由这 $C_n^2$ 个差按从小到大顺序排成的一个数列，称为集合 $A$ 的"衍生数列"，记为 $\overline{A}$．衍生数列 $\overline{A}$ 中能被 $m$ 整除的数的个数记为 $\overline{A}(m)$．
证明：对于任一正整数 $m\geqslant 2$，$n$ 元整数集 $A=\{a_1,a_2,\cdots,a_n\}$ 及集合 $B=\{1,2,\cdots,n\}$ 所对应的"衍生数列" $\overline{A}$ 及 $\overline{B}$，满足不等式 $\overline{A}(m)\geqslant\overline{B}(m)$．		 2022-04-17 19:27:46
18973 5d522871210b280220ed79c4 高中 解答题 自招竞赛 杰克船长与他的海岛们掠夺到 $6$ 个珍宝箱 $A_1,A_2,A_3,A_4,A_5,A_6$，其中 $A_i$ 内有金币 $a_i$ 枚，$i=1,2,3,4,5,6$，诸 $a_i$ 互不相等．海盗们设计了一种箱子的布局图（如图），并推派一人和船长轮流拿珠宝箱．每次可任意拿走不和两个或两个以上的箱子相连的整个箱子．如果船长最后所取得的金币不少于海盗们所取得的金币，那么船长获胜．
问：若船长先拿，他是否有适当的取法保证获胜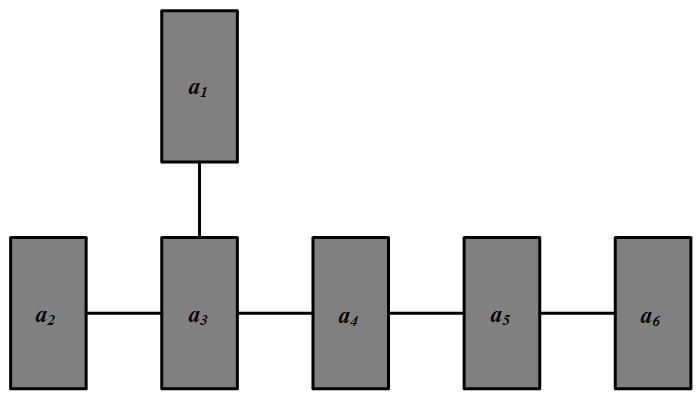？		 2022-04-17 19:26:46
18965 5d526e23210b280220ed7a37 高中 解答题 自招竞赛 试求最小的正整数 $n$，使得对于满足条件 $\displaystyle \sum\limits_{i=1}^na_i=200$ 的任一具有 $n$ 项的正整数数列 $a_1,a_2,\cdots,a_n$，其中必有连续的若干项之和等于 $30$． 2022-04-17 19:22:46
18957 5d539e2a210b280220ed7ad0 高中 解答题 自招竞赛 一副纸牌共 $52$ 张，其中"方块"，"梅花"，"红心"，"黑桃"每种花色的牌各 $13$ 张，标号依次是 $2,3,\cdots,10$，$J,Q,K,A$，其中相同花色，相邻标号的两张牌称为"同花顺牌"，并且 $A$ 与 $2$ 也算是顺牌（即 $A$ 可以当 $1$ 使用）．试确定，从这副牌中取出 $13$ 张牌，使每种标号的牌都出现，并且不含"同花顺牌"的取牌方法数． 2022-04-17 19:17:46
18952 5d53d570210b28021fc79a7b 高中 解答题 自招竞赛 对于周长为 $n(n\in N^{\ast})$ 的圆，称满足如下条件的最小的正整数 $P_n$ 为"圆剖分数"；如果在圆周上有 $P_n$ 个点 $A_1,A_2,\cdots,A_{P_n}$，对于 $1,2,\cdots,n-1$ 中的每一个整数 $m$，都存在两个点 $A_i,A_j(1\leqslant i,j\leqslant P_n)$，以 $A_i$ 和 $A_j$ 为端点的一条弧长等于 $m$；圆周上每相邻两点间的弧长顺次构成的序列 $T_n=(a_1,a_2,\cdots,a_{P_n})$ 称为"圆部分序列"．例如：当 $n=13$ 时，圆剖分数为 $P_{13}=4$，如图所示，图中所标数字为相邻两点之间的弧长，圆剖分序列为 $T_{13}=(1,3,2,7)$ 或 $(1,2,6,4)$．求 $P_{21}$ 和 $P_{31}$，并各给出一个相应的圆剖分序列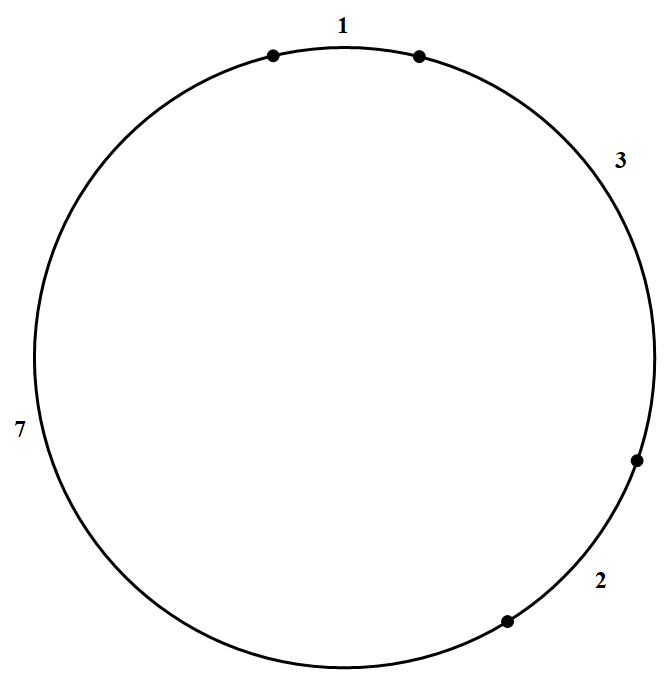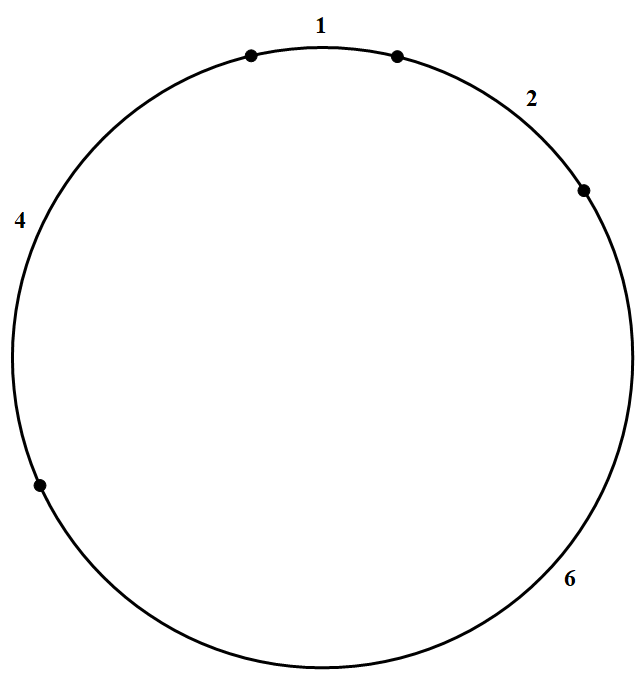． 2022-04-17 19:14:46
18912 5d54c764210b280220ed7bbe 高中 解答题 自招竞赛 设 $n$ 是正整数，集合 $M=\{1,2,\cdots,2n\}$．求最小的正整数 $k$，使得对于 $M$ 的任何一个 $k$ 元子集，其中必有 $4$ 个互不相同的元素之和等于 $4n+1$． 2022-04-17 19:51:45
18909 5d54f141210b28021fc79b4b 高中 解答题 自招竞赛 将数集 $A=\{a_1,a_2,\cdots,a_n\}$ 中所有元素的算术平均值记为 $P(A)\left(P(A)=\dfrac{a_1+a_2+\cdots+a_n}{n}\right)$．若 $B$ 是 $A$ 的非空子集，且 $P(B)=P(A)$，则称 $B$ 是 $A$ 的一个"均衡子集"．试求数集 $M=\{1,2,3,4,5,6,7,8,9\}$ 的所有"均衡子集"的个数． 2022-04-17 19:50:45
18869 5d561d9b210b28021fc79c10 高中 解答题 自招竞赛 给定大于 $2004$ 的正整数 $n$，将 $1,2,3,\cdots,n^2$ 分别填入 $n\times n$ 棋盘（由 $n$ 行 $n$ 列方格构成）的方格中，使每个方格恰有一个数．如果一个方格中填的数大于它所在行至少 $2004$ 个方格内所填的数，且大于它所在列至少 $2004$ 个方格内所填的数，则称这个方格为"优格"．求棋盘中"优格"个数的最大值． 2022-04-17 19:29:45
18866 5d5646e8210b280220ed7d4c 高中 解答题 自招竞赛 $n$ 支球队要举行主客场双循环比赛（每两支球队比赛两场，各有一场主场比赛），每支球队在一周（从周日到周六的七天）内可以进行多场客场比赛．但如果某周内该球队有主场比赛，在这一周内不能安排该球队的客场比赛．如果 $4$ 周内能完成全部比赛，求 $n$ 的最大值．
注：甲、乙两队在甲方场地举行的比赛，称为甲的主场比赛，乙的客场比赛．		 2022-04-17 19:26:45
18865 5d564c27210b280220ed7d64 高中 解答题 自招竞赛 求满足 $\dfrac{x-y}{x+y}+\dfrac{y-z}{y+z}+\dfrac{z-u}{z+u}+\dfrac{u-x}{u+x}>0$，且 $1\leqslant x,y,z,u\leqslant 10$ 的所有四元有序整数组 $(x,y,z,u)$ 的个数． 2022-04-17 19:26:45
18847 5d47bef5210b280220ed71f9 高中 解答题 自招竞赛 定义经过无穷多个整点的直线为好直线，已知任意平行于坐标轴的好直线都经过无穷多种颜色的整点（将平面上所有点染色），问：是否一定存在不平行于坐标轴的直线经过无穷多种颜色的整点． 2022-04-17 19:14:45
18842 5d492800210b28021fc794b7 高中 解答题 自招竞赛 已知正整数 $n,k$，对于一个 $n$ 顶点的树 $T$，标记它的顶点为 $1,2\cdots,n$ 序列 $(a_1,a_2,\cdots,a_k),1\leqslant a_i\leqslant n,1\leqslant i\leqslant k$．若 $a_i$ 与 $a_{i+1}(1\leqslant i\leqslant k-1')$ 在 $T$ 中相连，则可交换 $a_i$ 与 $a_{i+1}$ 称交换前后的两个序列为等价的，若两个序列可以通过若干步操作得到，称它们是等价的，记 $f(T)$ 为序列中等价类的个数，求 $f(T)$ 的可能值． 2022-04-17 19:10:45
18841 5c821398210b28428f14d323 高中 解答题 自招竞赛 我们称平面上一个有限点集 $S$ 是平衡的，如果对任意两个不同的点 $A,B$，都存在 $S$ 中一个点 $C$ 满足 $AC=BC$，我们称 $S$ 是无中心的，如果对 $S$ 中任意三个不同的点 $A,B,C$，都不存在 $S$ 中的一点 $P$，满足 $PA=PB=PC$．
（a）证明：对每个整数 $n\geqslant 3$，均存在一个由 $n$ 个点构成的平衡点集．
（b）确定所有的整数 $n\geqslant 3$，使得存在一个由 $n$ 个点构成的平衡且无中心的点集．（荷兰）		 2022-04-17 19:10:45
18837 5d566f2d210b28021fc79c55 高中 解答题 自招竞赛 一个反帕斯卡三角形是由一些数排成的等边三角形数阵，其中每个不在最后一行的数都恰好等于排在它下面的两个数的差的绝对值．例如，下面的数阵是一个反帕斯卡三角形，它共有四行，并且恰含有 $1$ 至 $10$ 中的每个整数．$$4\\2,6\\5,7,1\\8,3,10,9$$试问：是否存在一个共有 $2018$ 行的反帕斯卡三角形，恰含有 $1$ 至 $1+2+\cdots+2018$ 中的每个整数？（伊朗） 2022-04-17 19:07:45
18836 5d56714b210b28021fc79c5e 高中 解答题 自招竞赛 我们所谓一个位置是指直角坐标平面上的一个点 $(x,y)$，其中 $x,y$ 都是不超过 $20$ 的正整数．
最初时，所有 $400$ 个位置都是空的．甲乙两人轮流摆放石子，由甲先进行．每次轮到到甲时，他在一个空的位置上摆上一个新的红色石子，要求任意两个红色石子所在位置之间的距离都不等于 $\sqrt{5}$．每次轮到乙时．他在任意一个空的的位置上摆上一个新的蓝色石子．（蓝色石子所在位置与其他石子所在位置之间距离可以是任意值．）如此这般进行下去直至某个人无法再摆放石子．
试确定最大的整数 $K$，使得无论乙如何摆放蓝色石子，甲总能保证至少摆放 $K$ 个红色石子．（亚美尼亚）		 2022-04-17 19:06:45
18831 59bb3db177c760000717e40e 高中 解答题 自招竞赛 一名猎人和一只隐形兔在平面上玩游戏，兔子的起始点和猎人的起始点相同．经过 $n-1$ 轮游戏中，兔子在点 $A_{n-1}$ 而猎人在点 $B_{n-1}$，在第 $n$ 轮游戏中，依次发生以下三件事：
$(1)$ 兔子隐身移动到点 $A_n$，并满足 $A_{n-1}$ 与 $A_n$ 之间的距离恰好为 $1$，
$(2)$ 追踪设备报告给猎人一个点 $P_n$，该追踪设备只能保证 $P_n$ 与 $A_n$ 之间的距离不超过 $1$，
$(3) $ 猎人移动到点 $B_n$，并满足 $B_{n-1}$ 与 $B_n$ 之间的距离恰好为 $1$，
问是否存在这样的可能，不论兔子如何移动，并且不论追踪设备报告了什么点，猎人总可以选择他的移动方式，使得经过 $10^9$ 轮游戏后猎人与兔子之间的距离不超过 $100$．（奥地利）		 2022-04-17 19:04:45
18829 59bb3db177c760000717e412 高中 解答题 自招竞赛 给定整数 $n\geqslant 2$，已知 $n(n+1)$ 个身高两两不同的足球队员站成一排．球队教练Alex希望从这些球员中移走 $n(n-1)$ 人，使得这一排剩下的 $2n$ 名球员满足如下 $n$ 个条件：
$(1) $ 他们当中身高最高的两名球员之间没有别的球员；
$(2) $ 他们当中身高第三和第四的两名球员之间没有别的球员；
$\cdots$
$(n)$ 他们当中身高最矮的两名球员之间没有别的球员．
证明：这总是可以做到的．（俄罗斯）		 2022-04-17 19:03:45
0.171653s