在 $8\times 8$ 方格表中,最少需要挖去几个小方格,才能使得无法从剩余的方格表中剪裁出一片形状如图所示完整的 $T$ 形五方连块?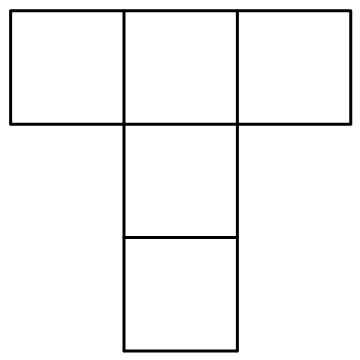

【难度】
【出处】
2009中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
至少要如图挖去 $14$ 个小方格. 如下图,将 $8\times 8$ 棋盘切为五个区域.
如下图,将 $8\times 8$ 棋盘切为五个区域. 中央部分的区域至少要挖去 $2$ 个小方格才能使 $T$ 形的五方块放不进去.两个打叉的位置是不等同的位置,一个是在角落位置,另一个是内部位置,只挖去其中一个无法避免 $T$ 置入,如下图所示.
中央部分的区域至少要挖去 $2$ 个小方格才能使 $T$ 形的五方块放不进去.两个打叉的位置是不等同的位置,一个是在角落位置,另一个是内部位置,只挖去其中一个无法避免 $T$ 置入,如下图所示. 对于在边界的四个全等的区域,每区域至少要挖去 $3$ 个小方格才能使 $T$ 形的五方块放不进去.
对于在边界的四个全等的区域,每区域至少要挖去 $3$ 个小方格才能使 $T$ 形的五方块放不进去.
证明:以右上角的区域为例(下图),下方 $T$ 形部分必须挖去 $1$ 个小方格,上方部分必须挖去打叉位置的 $1$ 个小方格.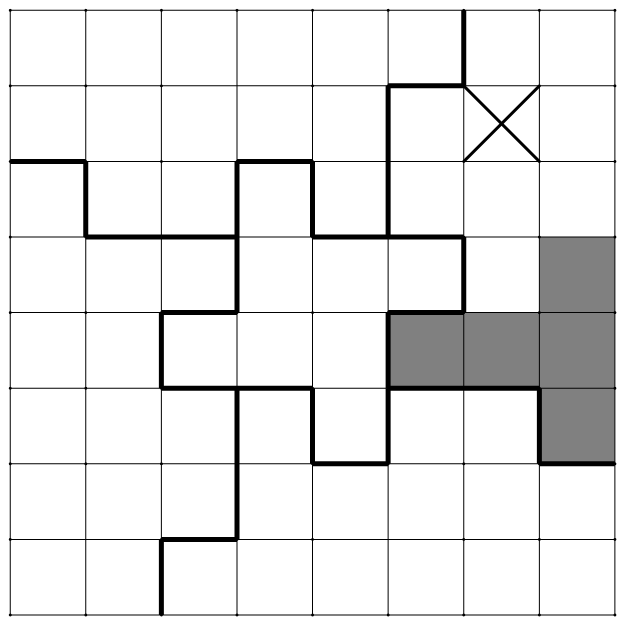 下方 $T$ 形部分挖去的 $1$ 个小方格有五种情况(下图),但无论如何均可再置入一片 $T$ 形的五方块,因此至少要挖去 $3$ 个小方格.
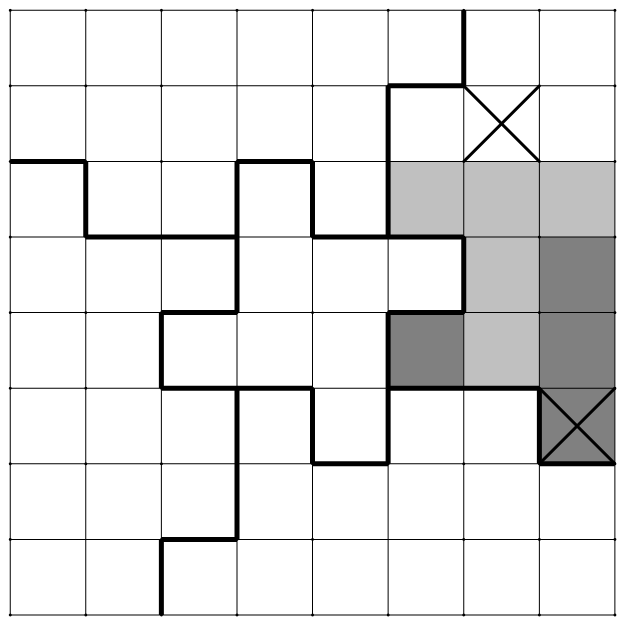
下方 $T$ 形部分挖去的 $1$ 个小方格有五种情况(下图),但无论如何均可再置入一片 $T$ 形的五方块,因此至少要挖去 $3$ 个小方格.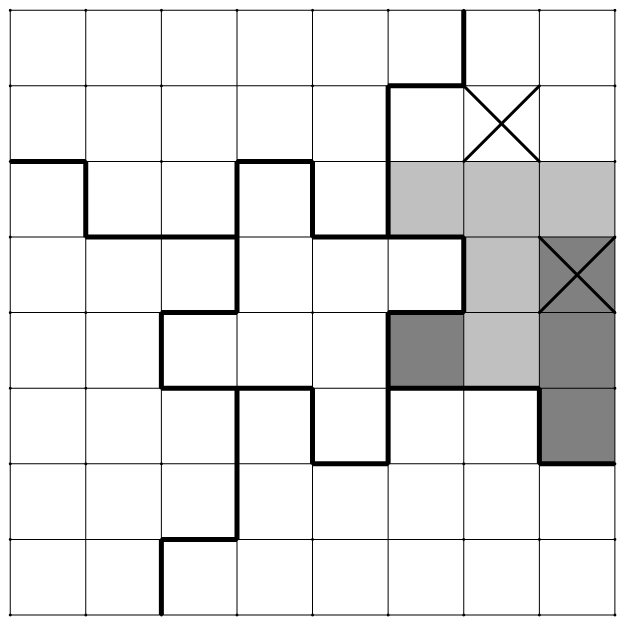

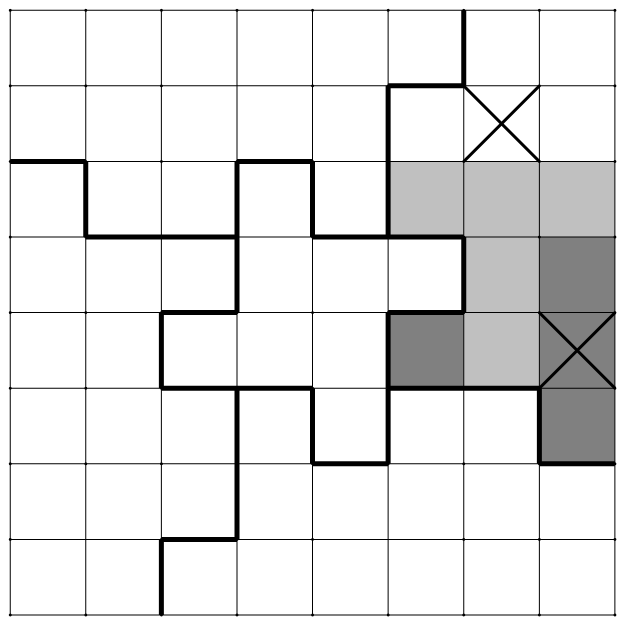

 综合所有区域,对于 $T$ 形五方块至少要挖去 $3\times 4+2-14$(个)小方格.
综合所有区域,对于 $T$ 形五方块至少要挖去 $3\times 4+2-14$(个)小方格.
 如下图,将 $8\times 8$ 棋盘切为五个区域.
如下图,将 $8\times 8$ 棋盘切为五个区域. 中央部分的区域至少要挖去 $2$ 个小方格才能使 $T$ 形的五方块放不进去.两个打叉的位置是不等同的位置,一个是在角落位置,另一个是内部位置,只挖去其中一个无法避免 $T$ 置入,如下图所示.
中央部分的区域至少要挖去 $2$ 个小方格才能使 $T$ 形的五方块放不进去.两个打叉的位置是不等同的位置,一个是在角落位置,另一个是内部位置,只挖去其中一个无法避免 $T$ 置入,如下图所示. 对于在边界的四个全等的区域,每区域至少要挖去 $3$ 个小方格才能使 $T$ 形的五方块放不进去.
对于在边界的四个全等的区域,每区域至少要挖去 $3$ 个小方格才能使 $T$ 形的五方块放不进去.证明:以右上角的区域为例(下图),下方 $T$ 形部分必须挖去 $1$ 个小方格,上方部分必须挖去打叉位置的 $1$ 个小方格.
 下方 $T$ 形部分挖去的 $1$ 个小方格有五种情况(下图),但无论如何均可再置入一片 $T$ 形的五方块,因此至少要挖去 $3$ 个小方格.
下方 $T$ 形部分挖去的 $1$ 个小方格有五种情况(下图),但无论如何均可再置入一片 $T$ 形的五方块,因此至少要挖去 $3$ 个小方格.




 综合所有区域,对于 $T$ 形五方块至少要挖去 $3\times 4+2-14$(个)小方格.
综合所有区域,对于 $T$ 形五方块至少要挖去 $3\times 4+2-14$(个)小方格.
答案
解析
备注