对于周长为 $n(n\in N^{\ast})$ 的圆，称满足如下条件的最小的正整数 $P_n$ 为"圆剖分数"；如果在圆周上有 $P_n$ 个点 $A_1,A_2,\cdots,A_{P_n}$，对于 $1,2,\cdots,n-1$ 中的每一个整数 $m$，都存在两个点 $A_i,A_j(1\leqslant i,j\leqslant P_n)$，以 $A_i$ 和 $A_j$ 为端点的一条弧长等于 $m$；圆周上每相邻两点间的弧长顺次构成的序列 $T_n=(a_1,a_2,\cdots,a_{P_n})$ 称为"圆部分序列"．例如：当 $n=13$ 时，圆剖分数为 $P_{13}=4$，如图所示，图中所标数字为相邻两点之间的弧长，圆剖分序列为 $T_{13}=(1,3,2,7)$ 或 $(1,2,6,4)$．求 $P_{21}$ 和 $P_{31}$，并各给出一个相应的圆剖分序列．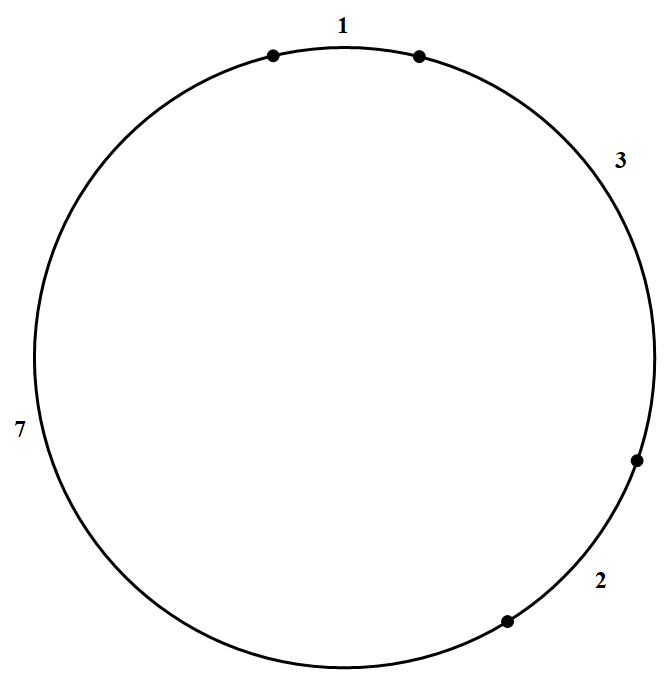
【难度】
【出处】
2006中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
由于 $k$ 个点中，每两个点间可得一段优弧和一段劣弧，故至多可得 $k(k-1)$ 个弧长值．
当 $k(k-1)\geqslant 20$ 时，$k\geqslant 5$；
而当 $k(k-1)\geqslant 30$ 时，$k\geqslant 6$．
另一方面，在 $k=5$ 时，可以给出剖分图．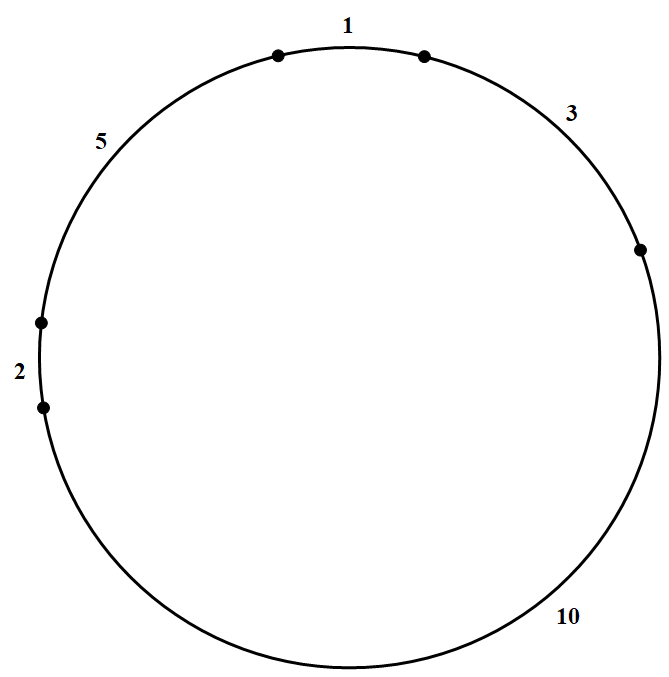
所以，$P_{21}=5,T_{21}=(1,3,10,2,5)$．
对于 $n=31$，在 $k=6$ 时，类似可给出剖分图．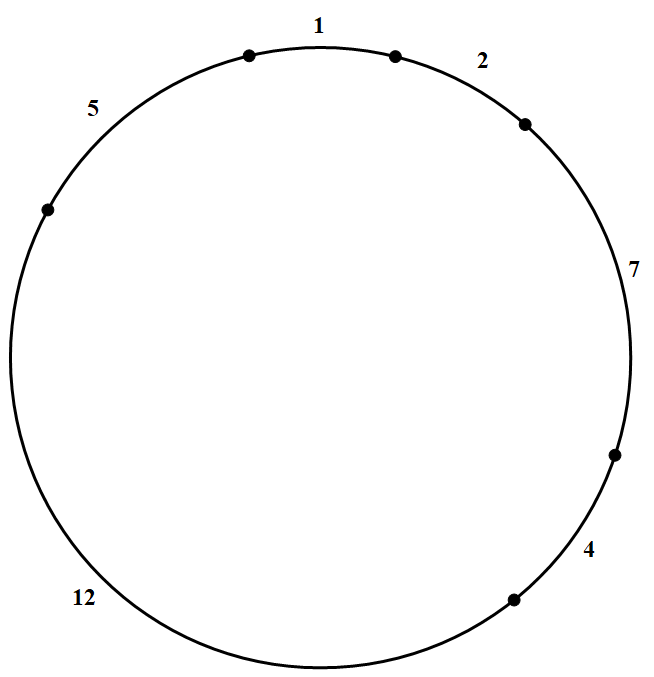
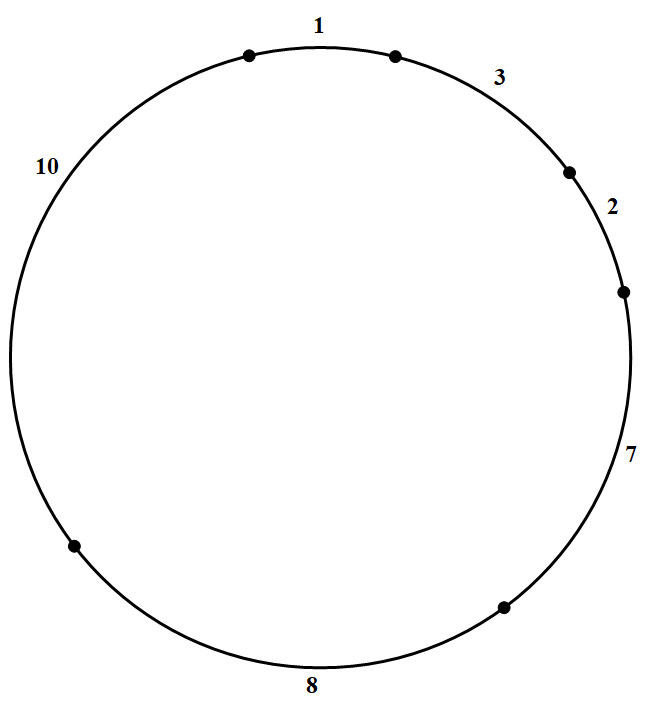
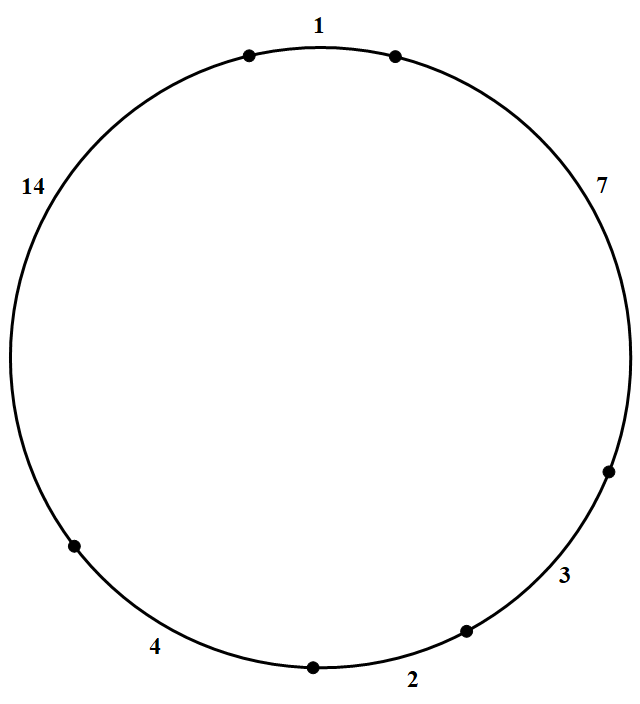所以 $P_{31}=6$
$T_{31}=(1,2,7,4,12,5),(1,2,5,4,6,13),(1,3,2,7,8,10),(1,3,6,2,5,14)$ 或 $(1,7,3,2,4,14)$ 等．
当 $k(k-1)\geqslant 20$ 时，$k\geqslant 5$；
而当 $k(k-1)\geqslant 30$ 时，$k\geqslant 6$．
另一方面，在 $k=5$ 时，可以给出剖分图．
所以，$P_{21}=5,T_{21}=(1,3,10,2,5)$．对于 $n=31$，在 $k=6$ 时，类似可给出剖分图．
所以 $P_{31}=6$$T_{31}=(1,2,7,4,12,5),(1,2,5,4,6,13),(1,3,2,7,8,10),(1,3,6,2,5,14)$ 或 $(1,7,3,2,4,14)$ 等．
答案
解析
备注
