一名猎人和一只隐形兔在平面上玩游戏，兔子的起始点和猎人的起始点相同．经过 $n-1$ 轮游戏中，兔子在点 $A_{n-1}$ 而猎人在点 $B_{n-1}$，在第 $n$ 轮游戏中，依次发生以下三件事：
$(1)$ 兔子隐身移动到点 $A_n$，并满足 $A_{n-1}$ 与 $A_n$ 之间的距离恰好为 $1$，
$(2)$ 追踪设备报告给猎人一个点 $P_n$，该追踪设备只能保证 $P_n$ 与 $A_n$ 之间的距离不超过 $1$，
$(3) $ 猎人移动到点 $B_n$，并满足 $B_{n-1}$ 与 $B_n$ 之间的距离恰好为 $1$，
问是否存在这样的可能，不论兔子如何移动，并且不论追踪设备报告了什么点，猎人总可以选择他的移动方式，使得经过 $10^9$ 轮游戏后猎人与兔子之间的距离不超过 $100$．（奥地利）
$(1)$ 兔子隐身移动到点 $A_n$，并满足 $A_{n-1}$ 与 $A_n$ 之间的距离恰好为 $1$，
$(2)$ 追踪设备报告给猎人一个点 $P_n$，该追踪设备只能保证 $P_n$ 与 $A_n$ 之间的距离不超过 $1$，
$(3) $ 猎人移动到点 $B_n$，并满足 $B_{n-1}$ 与 $B_n$ 之间的距离恰好为 $1$，
问是否存在这样的可能，不论兔子如何移动，并且不论追踪设备报告了什么点，猎人总可以选择他的移动方式，使得经过 $10^9$ 轮游戏后猎人与兔子之间的距离不超过 $100$．（奥地利）
【难度】
【出处】
2017年第58届IMO试题
【标注】
【答案】
不存在
【解析】
不存在．为了证明这一结论，可以假定兔子可以按约定的方式为追踪设备指定 $P_n$ 的位置．
首先，在开局的时候，兔子指定 $P_1=A_0$，此时猎人只能随机选择一个方向移动，对兔子最有利的情形下 $|A_1B_1|=2$；
接下来研究当 $|A_kB_k|=d$（$d\leqslant 101$）时，兔子进一步增加两者之间的距离的方案．如图，兔子沿着直角三角形的斜边移动，而指定追踪设备依次报告它在 $\overrightarrow{B_kA_k}$ 方向上的投影的位置，且 $A_{k+t}P_{k+t}=1$，$A_{k+t}A_k=t$．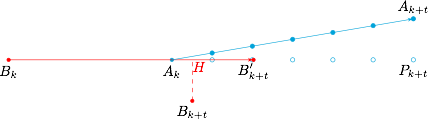
这样猎人的最佳策略就是沿 $\overrightarrow{B_kA_k}$ 方向持续追击 $t$ 步，到达 $B_{k+t}'$ 的位置．否则根据对称性，猎人所选择的策略的最坏结果是 $B_{k+t}$ 与 $A_{k+t}$ 在 $\overrightarrow{B_kA_k}$ 方向的两侧，此时有\[A_{k+t}B_{k+t}>A_{k+t}H>A_{k+t}B_{k+t}',\]其中 $H$ 为 $B_{k+t}$ 在 $\overrightarrow{B_kA_k}$ 方向上的投影．
我们来计算经过 $t$ 步后，兔子和猎人之间的距离增加量\[\begin{split}
A_{k+t}B_{k+t}'-A_kB_k&=\sqrt{1+\left(d+\sqrt{t^2-1}-t\right)^2}-d\\
&=\sqrt{1+\left(d-\dfrac{1}{t+\sqrt{t^2-1}}\right)^2}-d\\
&=\sqrt{d^2-\dfrac{2d}{t+\sqrt{t^2-1}}+\dfrac{2t^2+2t\sqrt{t^2-1}}{\left(t+\sqrt{t^2-1}\right)^2}}-d\\
&=\sqrt{d^2+\dfrac{2(t-d)}{t+\sqrt{t^2-1}}}-d\\
&>\sqrt{d^2+1-\dfrac{d}{t}}-d\\
&=\dfrac{1-\dfrac dt}{\sqrt{d^2+1-\dfrac dt}+d}
,\end{split}\]由于 $d\leqslant 101$，取 $t=202$，于是\[A_{k+t}B_{k+t}'-A_kB_k>\dfrac{1-\dfrac dt}{2d+1}\geqslant \dfrac{1}{406},\]因此兔子经过\[(102-2)\cdot 406\cdot 202+1=8201201\]步后与猎人的距离必然大于 $101$．
由于兔子在与猎人的距离大于 $101$ 后可以按照猎人上次的移动的方式进行移动，这就意味着不存在猎人在 $10^9$ 轮游戏后与兔子的距离不超过 $100$ 的必然方案．
首先，在开局的时候，兔子指定 $P_1=A_0$，此时猎人只能随机选择一个方向移动，对兔子最有利的情形下 $|A_1B_1|=2$；
接下来研究当 $|A_kB_k|=d$（$d\leqslant 101$）时，兔子进一步增加两者之间的距离的方案．如图，兔子沿着直角三角形的斜边移动，而指定追踪设备依次报告它在 $\overrightarrow{B_kA_k}$ 方向上的投影的位置，且 $A_{k+t}P_{k+t}=1$，$A_{k+t}A_k=t$．
这样猎人的最佳策略就是沿 $\overrightarrow{B_kA_k}$ 方向持续追击 $t$ 步，到达 $B_{k+t}'$ 的位置．否则根据对称性，猎人所选择的策略的最坏结果是 $B_{k+t}$ 与 $A_{k+t}$ 在 $\overrightarrow{B_kA_k}$ 方向的两侧，此时有\[A_{k+t}B_{k+t}>A_{k+t}H>A_{k+t}B_{k+t}',\]其中 $H$ 为 $B_{k+t}$ 在 $\overrightarrow{B_kA_k}$ 方向上的投影．我们来计算经过 $t$ 步后，兔子和猎人之间的距离增加量\[\begin{split}
A_{k+t}B_{k+t}'-A_kB_k&=\sqrt{1+\left(d+\sqrt{t^2-1}-t\right)^2}-d\\
&=\sqrt{1+\left(d-\dfrac{1}{t+\sqrt{t^2-1}}\right)^2}-d\\
&=\sqrt{d^2-\dfrac{2d}{t+\sqrt{t^2-1}}+\dfrac{2t^2+2t\sqrt{t^2-1}}{\left(t+\sqrt{t^2-1}\right)^2}}-d\\
&=\sqrt{d^2+\dfrac{2(t-d)}{t+\sqrt{t^2-1}}}-d\\
&>\sqrt{d^2+1-\dfrac{d}{t}}-d\\
&=\dfrac{1-\dfrac dt}{\sqrt{d^2+1-\dfrac dt}+d}
,\end{split}\]由于 $d\leqslant 101$，取 $t=202$，于是\[A_{k+t}B_{k+t}'-A_kB_k>\dfrac{1-\dfrac dt}{2d+1}\geqslant \dfrac{1}{406},\]因此兔子经过\[(102-2)\cdot 406\cdot 202+1=8201201\]步后与猎人的距离必然大于 $101$．
由于兔子在与猎人的距离大于 $101$ 后可以按照猎人上次的移动的方式进行移动，这就意味着不存在猎人在 $10^9$ 轮游戏后与兔子的距离不超过 $100$ 的必然方案．
答案
解析
备注
