杰克船长与他的海岛们掠夺到 $6$ 个珍宝箱 $A_1,A_2,A_3,A_4,A_5,A_6$，其中 $A_i$ 内有金币 $a_i$ 枚，$i=1,2,3,4,5,6$，诸 $a_i$ 互不相等．海盗们设计了一种箱子的布局图（如图），并推派一人和船长轮流拿珠宝箱．每次可任意拿走不和两个或两个以上的箱子相连的整个箱子．如果船长最后所取得的金币不少于海盗们所取得的金币，那么船长获胜．
问：若船长先拿，他是否有适当的取法保证获胜？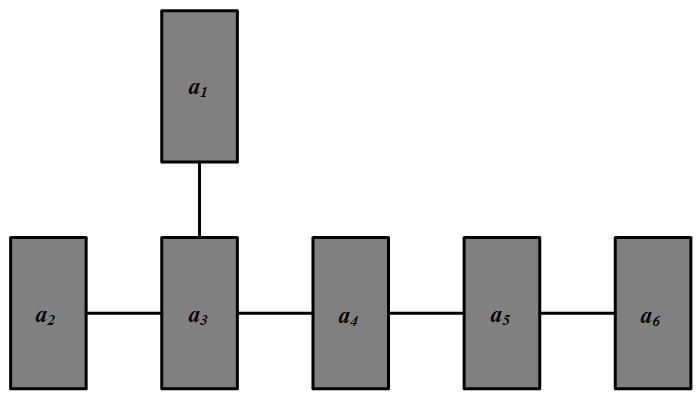
问：若船长先拿，他是否有适当的取法保证获胜？
【难度】
【出处】
2008中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
当箱子数为 $2$ 时，船长有必胜之策略．
引理一：当箱子数为 $4$ 时，船长有必胜之策略．
当箱子数为 $4$ 时，共有两种不同的链接在一起的方式．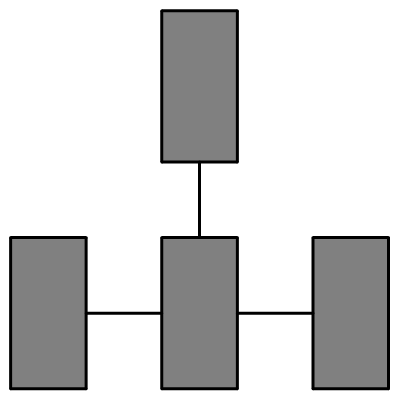
$$第一种情况$$
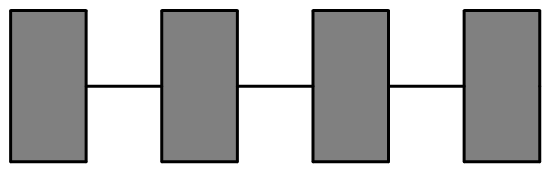$$第二种情况$$第一种情况时：
在开始的第一轮船长有在外部的三个箱子可挑选，船长当然挑选这三个箱子中最多金币的箱子，海盗只能拿剩下来的两个箱子之一，无法取得中央的箱子．经过第一轮后，船长拿到的金币不少于海盗，此时剩下两个箱子，船长可以拿金币较多的箱子，因此船长必胜．
第二种情况时：
将 $4$ 个箱子黑白相间涂色，如下图所示：
若在两个涂黑色箱子内金币的数量总和不少于两个涂白色箱子内金币的数量总和和，则开始时船长所能拿到的黑色箱子，迫使海盗接下来只能取白色箱子，当海盗拿完后又露出一个黑色箱子让船长拿，从而船长可拿光所有黑色箱子而获胜．否则船长可以拿光所有白色箱子而获胜．
回到原题．
假设 $a_6$ 内金币的数量不小于 $a_5$，则船长先取能拿到的箱子中最多金币的一个箱子，海盗拿后，还剩四个箱子．问题转化为四个箱子的情形．
假设 $a_5$ 内金币的数量多于 $a_6$，且不妨假设 $a_1$ 内金币的数量比 $a_2$ 多，则船长将 $a_1,a_3$ 与 $a_5$ 涂白色，其他的箱子涂黑色，如下图所示．
现在检验涂白色箱子内金币的数量总和是否不少于涂黑色箱子内金币的数量总和．若是，则船长能拿光所有白色箱子而获胜．若否，则船长先拿 $a_6$，接下来：
（1）若海盗拿 $a_1$，则船长再依次拿 $a_2,a_4$ 而获胜．
（2）若海盗拿 $a_2$，已知 $a_1$ 内金币的数量比 $a_2$ 多，则船长接着拿 $a_1$．虽然船长不能拿光所有黑色箱子，但因为 $a_1$ 内金币的数量比 $a_2$ 多，二者替换之后船长一点都不吃亏，最终仍然可获胜．
（3）若海盗拿 $a_5$，则船长接着拿 $a_4$，接着：
① 若海盗拿 $a_1$，则船长拿 $a_2$ 而获胜．
② 若海盗拿 $a_2$，已知 $a_1$ 内金币的数量比 $a_2$ 多，则船长接着拿 $a_1$，可获胜．
故不论原先箱子内的金币数为多少，船长均有恰当的取法保证获胜．
引理一：当箱子数为 $4$ 时，船长有必胜之策略．
当箱子数为 $4$ 时，共有两种不同的链接在一起的方式．
$$第一种情况$$$$第二种情况$$第一种情况时：在开始的第一轮船长有在外部的三个箱子可挑选，船长当然挑选这三个箱子中最多金币的箱子，海盗只能拿剩下来的两个箱子之一，无法取得中央的箱子．经过第一轮后，船长拿到的金币不少于海盗，此时剩下两个箱子，船长可以拿金币较多的箱子，因此船长必胜．
第二种情况时：
将 $4$ 个箱子黑白相间涂色，如下图所示：
若在两个涂黑色箱子内金币的数量总和不少于两个涂白色箱子内金币的数量总和和，则开始时船长所能拿到的黑色箱子，迫使海盗接下来只能取白色箱子，当海盗拿完后又露出一个黑色箱子让船长拿，从而船长可拿光所有黑色箱子而获胜．否则船长可以拿光所有白色箱子而获胜．回到原题．
假设 $a_6$ 内金币的数量不小于 $a_5$，则船长先取能拿到的箱子中最多金币的一个箱子，海盗拿后，还剩四个箱子．问题转化为四个箱子的情形．
假设 $a_5$ 内金币的数量多于 $a_6$，且不妨假设 $a_1$ 内金币的数量比 $a_2$ 多，则船长将 $a_1,a_3$ 与 $a_5$ 涂白色，其他的箱子涂黑色，如下图所示．
现在检验涂白色箱子内金币的数量总和是否不少于涂黑色箱子内金币的数量总和．若是，则船长能拿光所有白色箱子而获胜．若否，则船长先拿 $a_6$，接下来：（1）若海盗拿 $a_1$，则船长再依次拿 $a_2,a_4$ 而获胜．
（2）若海盗拿 $a_2$，已知 $a_1$ 内金币的数量比 $a_2$ 多，则船长接着拿 $a_1$．虽然船长不能拿光所有黑色箱子，但因为 $a_1$ 内金币的数量比 $a_2$ 多，二者替换之后船长一点都不吃亏，最终仍然可获胜．
（3）若海盗拿 $a_5$，则船长接着拿 $a_4$，接着：
① 若海盗拿 $a_1$，则船长拿 $a_2$ 而获胜．
② 若海盗拿 $a_2$，已知 $a_1$ 内金币的数量比 $a_2$ 多，则船长接着拿 $a_1$，可获胜．
故不论原先箱子内的金币数为多少，船长均有恰当的取法保证获胜．
答案
解析
备注
